 |
Exercises and problems in Informatics |
Please read The Conditions of the Problem Solving Competition.
I. 58. A sequence a1, a2, ..., an of positive integers each having at most N digits is called an aliquot sequence of N digits, if the sum of positive proper divisors (i.e. including 1 but excluding the number itself) of ai is ai+1 (i=1,2,...,n-1) and that of an is a1. Members of an aliquot sequence are called sociable numbers. (Thus, the aliquot sequences of length 1 are just the perfect numbers, and aliquot sequences of length 2 are the usual amicable pairs.)
Your program (i58.pas, ...) should read the value of N (1\(\displaystyle \le\)N \(\displaystyle \le\)8), compute every sociable numbers of N digits for which the smallest element is in the interval [A,B], then write the output into the text file ``i58.out''.
The file containing the output corresponding to parameter values N=7, A=2, B=9 999 999 should be submitted.
Examples. Sociable numbers of 3 digits with the smallest element in the interval [200,230] form the well-known amicable pair 220-284.
Sociable numbers of 5 digits with the smallest element in the interval [10000,13000] include 10744-10856, 12285-14595, 12496-14288-15472-14536-14264.
(10 points)
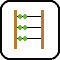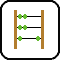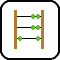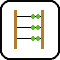
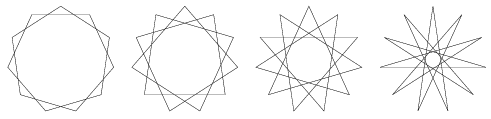
I. 59. A regular star polygon with N vertices is obtained by connecting every vertex of a regular N-gon with both of its Kth neighbours.
Write a program (i59.pas, ...) which reads the value of N (5\(\displaystyle \le\)N \(\displaystyle \le\)100), then displays all distinct regular star polygons with N vertices.
The example shows all 4 distinct regular star polygons with 11 vertices.
(10 points)
I. 60. Similarly to the concept of highly composite numbers (see Problem I. 55. in the September 2003 issue), we say that a positive integer n \(\displaystyle \in\)[A,B] is highly composite with respect to the interval [A,B], if the number of divisors of n is greater than or equal to that of any positive integers in the interval [A,B] below n.
Prepare your sheet (i60.xls) which - if A and B (1\(\displaystyle \le\)A\(\displaystyle \le\)B\(\displaystyle \le\)1000) are given - displays all numbers in the interval [A,B] highlighting with red all highly composite numbers with respect to that interval.
In the example italic letters show the red highlighting.
| A=10 | B=25 |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 |
(10 points)
