 |
Solutions for advanced problems "A" in November, 2003 |
In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.
A. 329. A circle k1 of the plane lies in the interior of a circle k2. Point P lies inside k1, and point Q lies outside k2 in the plane. Given the circles and the points, draw an arbitrary line e through P that does not pass through Q. Let e intersect k1 at A and B. Let the circumscribed circle of ABQ intersect k2 at C and D. Prove that all line segments CD obtained in this way are concurrent.
Solution. Denote the intersection between line PQ and circles k1 and k2 and the crcumcircle k of ABC by E, F, G, H and R (see Figure 1). Points Q, G, E, P, F, H are indepentent of the choice of line e and they have always this order.
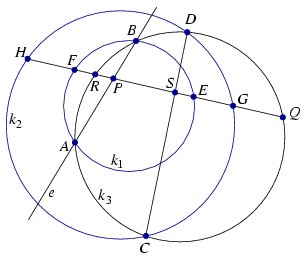
Figure 1
From the power of P to circles k1 and k3, PE.PF=PA.PB = PQ.PR. Therefore, the signed distance \(\displaystyle PR=\frac{PE\cdot PF}{PQ}\) is constant and point R is fixed. R is an interior point of PF, since \(\displaystyle 0<\frac{PR}{PF}=\frac{PE}{PQ}<1\). This implies that R lies inside k1 and k2.
Point P lies between A and B because it is an interior point of k1; hence, line PQ separates A and B. Consider the three arcs of k3 bounded by points A, B and Q. Points A and B lie inside k2, Q is outside. Therefore, k2 intersects arcs QA and QB; C and D lie in these arcs. Hence,points Q, D, B, R, A and C have always this order on circle k3 and the line segments CD and PR intersect each other. Denote their intersection point by S.
From the power of S to the circles, SG.SH=SC.SD=SQ.SR. The power is negative, thus S lies inside line segments QR and GH and thus GR. Epressing the signed distances SH and SR with SG,
SG.SH=SQ.SR
SG.(SG-HG)=(SG+GQ).(SG-RG)
\(\displaystyle SG=\frac{RG\cdot GQ}{HG+GQ-RG}=\frac{RG\cdot CQ}{HR+GQ}.\)
The signed distance SG does not depend on the choice of line e, S is the common point of all lin segments CD.
A. 330. The sequence of Lucas numbers is defined by the following recurrence: L0=2, L1=1, Ln+1=Ln+Ln-1. Show that L(p+1)/2p-1 is divisible by Lp for all primes p>3.
Solution. From the properties of p we only need that p is odd and not divisible by 3.
Let \(\displaystyle \alpha={1+\sqrt5\over2}\) and \(\displaystyle \beta={1-\sqrt5\over2}\); then
| (1) | Ln=\(\displaystyle \alpha\)n+\(\displaystyle \beta\)n. |
The definition and formula (1) can be extended to negative indices as well.
It is easy to check that LmLn=Lm+n+(-1)mLn-m of all itegers m,n. This implies
Ln+2m\(\displaystyle \equiv\)(-1)m+1Ln (mod Lm);
specially,
| (2) | Ln+2p\(\displaystyle \equiv\)Ln (mod Lp). |
Let k=(p+1)/2. Then
| (3) | \(\displaystyle L_k^p=(\alpha^k+\beta^k)^p= \sum_{m=0}^p{p\choose m}\alpha^{(p-m)k}\beta^{mk}=\) |
\(\displaystyle =\sum_{m=0}^{k-1}(-1)^{mk}{p\choose m}\alpha^{(p-2m)k} +\sum_{m=k}^p(-1)^{(p-m)k}{p\choose m}\beta^{(2m-p)k}=\)
\(\displaystyle =\sum_{m=0}^{k-1}(-1)^{mk}{p\choose m}L_{(p-2m)k} =\sum_{m=0}^{k-1}(-1)^{mk}{p\choose m}L_{(k-m)p-m}.\)
If m and k have opposite parities then
(-1)mkL(k-m)p-m = L(k-m)p-m \(\displaystyle \equiv\)Lp-m (mod Lp).
Otherwise, if k and m have the same parity then
(-1)mkL(k-m)p-m \(\displaystyle \equiv\)(-1)mL-m = Lm (mod Lp).
Substituting these into (3),
\(\displaystyle 2L_k^p\equiv2\sum_{\begin{matrix}0\le m\le p\cr m\equiv k~(2)\cr\end{matrix}} {p\choose m}L_m= 2\sum_{\begin{matrix}0\le m\le p\cr m\equiv k~(2)\cr\end{matrix}} {p\choose m}(\alpha^m+\beta^m)=\)
=((\(\displaystyle \alpha\)+1)p+(-1)k(\(\displaystyle \alpha\)-1)p)+((\(\displaystyle \beta\)+1)p+(-1)k(\(\displaystyle \beta\)-1)p)=
=(\(\displaystyle \alpha\)2p+\(\displaystyle \beta\)2p)+(-1)k(\(\displaystyle \alpha\)-p+\(\displaystyle \beta\)-p)=L2p+(-1)k+pLp\(\displaystyle \equiv\)L0=2 (mod Lp).
Since Lp is odd (Ln is even if and only if 3|n), this implies Lkp\(\displaystyle \equiv\)1 (mod Lp).
A. 331. According to the records of the Bureau of Statistics in Quasiland, any pair of citizens who know each other have exactly one common acquaintance, while any two people who do not know each other have at least ten common acquaintances. Is it possible that the records are accurate?
Solution. We show an eample for such a graph.
Let S be a set of 3n elements where n\(\displaystyle \ge\)9. Let the vertices of the graph be the n-element subset. Let two vertices be connected if the corresponding subsets are disjoint. This system has the required properties.
