 |
A 2003 novemberi A-jelű matematika feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
A. 329. Adott a síkban a k2 kör és a belsejében a k1 kör, valamint a P és Q pontok úgy, hogy a P pont a k1 belsejében, a Q pont pedig a k2 körön kívül helyezkedik el. Húzzunk P-n át egy tetszőleges e egyenest, amely nem megy át a Q ponton; legyenek k1 és e metszéspontjai A és B. Az ABQ háromszög körülírt köre messe a k2 kört a C és D pontokban. Mutassuk meg, hogy az így kapható CD szakaszok egy ponton mennek át.
Megoldás. Legyenek a PQ egyenes metszéspontjai a k1, k2 körökkel és az ABQ háromszög köré írt k3 körrel E, F, G, H és R az 1. ábra szerint. A Q, G, E, P, F, H pontok az e egyenes választásától nem függnek, és mindig ebben a sorrendben helyezkednek el.
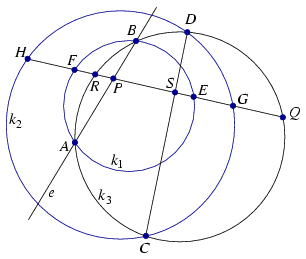
1. ábra
A P pontnak a k1 és k3 körökre vonatkozó hatványából PE.PF =PA.PB = PQ.PR. Ebből következik, hogy a \(\displaystyle PR=\frac{PE\cdot PF}{PQ}\) előjeles távolság állandó, és így az R pont is rögzített. Az R pont a PF szakasznak belső pontja, mert \(\displaystyle 0<\frac{PR}{PF}=\frac{PE}{PQ}<1\). Ebből következik, hogy R pont belső pontja a k1 és a k2 köröknek is.
A P pont az AB szakasz belsejébe esik, mert P belső pontja k1-nek; az A és B pontokat ezért a PQ egyenes elválasztja. Tekintsük azt a három körívet, amelyre a k3 kört az A, B és Q pontok felosztják. Az A és B pontok a k2 belsejében vannak, a Q pont pedig kívül. Ebből következik, hogy a három ív közül a QA és QB ívek metszik a k2 kört, tehát a C és D pontok ezen a két köríven helyezkednek el. A Q, D, B, R, A és C pontok tehát mindig az ábrán látható sorrendben követik egymást a k3 körön. Ebből következik, hogy a CD és PR szakaszok metszik egymást. A metszéspontot jelöljük S-sel.
Azt állítjuk, hogy az S pont sem függ az e egyenes megválasztásától. Az S pontnak a k2 és k3 körökre vonatkozó hatványából SG.SH=SC.SD=SQ.SR. Az előjeles szorzat negatív, ezért az S pont a QR és a GH szakasznak is belső pontja, tehát a PQ egyenesen G és R között helyezkedik el. Az SG szakasz előjeles hosszával kifejezve az SH, SH és SQ előjeles távolságokat,
SG.SH=SQ.SR
SG.(SG-HG)=(SG+GQ).(SG-RG)
\(\displaystyle SG=\frac{RG\cdot GQ}{HG+GQ-RG}=\frac{RG\cdot CQ}{HR+GQ}.\)
Az SG szakasz előjeles hossza tehát álandó, az S pont nem függ az e egyenes megválasztásától.
Megjegyzés. Több versenyző elfeledkezett a pontok lehetséges helyzeteinek vizsgálatáról, és csak annyit bizonyított be, hogy a CD egyenesek egy ponton mennek át. Ők 4 pontot kaptak.
A. 330. A Lucas-számok sorozatát a következő rekurzióval definiáljuk: L0=2, L1=1, Ln+1=Ln+Ln-1. Mutassuk meg, hogy tetszőleges p>3 prímszám esetén L(p+1)/2p-1 osztható Lp-vel.
Megoldás. A p szám tulajdonságaiból csak annyit fogunk felhasználni, hogy páratlan és nem osztható 3-mal.
Legyen \(\displaystyle \alpha={1+\sqrt5\over2}\) és \(\displaystyle \beta={1-\sqrt5\over2}\). Ekkor, mint ismeretes,
| (1) | Ln=\(\displaystyle \alpha\)n+\(\displaystyle \beta\)n. |
A Lucas számok sorozatát negatív indexekre is kiterjeszthetjük akár a rekurzió, akár az (1) képlet alapján.
Az (1) azonosságból könnyen ellenőrizhető, hogy tetszőleges m,n egész számok esetén LmLn=Lm+n+(-1)mLn-m; ebből következik, hogy
Ln+2m\(\displaystyle \equiv\)(-1)m+1Ln (mod Lm);
speciálisan,
| (2) | Ln+2p\(\displaystyle \equiv\)Ln (mod Lp). |
Legyen k=(p+1)/2. Az (1) azonosságot többször felhasználva,
| (3) | \(\displaystyle L_k^p=(\alpha^k+\beta^k)^p= \sum_{m=0}^p{p\choose m}\alpha^{(p-m)k}\beta^{mk}=\) |
\(\displaystyle =\sum_{m=0}^{k-1}(-1)^{mk}{p\choose m}\alpha^{(p-2m)k} +\sum_{m=k}^p(-1)^{(p-m)k}{p\choose m}\beta^{(2m-p)k}=\)
\(\displaystyle =\sum_{m=0}^{k-1}(-1)^{mk}{p\choose m}L_{(p-2m)k} =\sum_{m=0}^{k-1}(-1)^{mk}{p\choose m}L_{(k-m)p-m}.\)
Azokban az esetekben, amikor m és k ellentétes paritású, (-1)mk=1 és
(-1)mkL(k-m)p-m = L(k-m)p-m \(\displaystyle \equiv\)Lp-m (mod Lp).
Ha pedig k és m azonos paritású, akkor
(-1)mkL(k-m)p-m \(\displaystyle \equiv\)(-1)mL-m = Lm (mod Lp).
Ezeket behelyettesítve (3)-ba,
\(\displaystyle 2L_k^p\equiv2\sum_{\begin{matrix}0\le m\le p\cr m\equiv k~(2)\cr\end{matrix}} {p\choose m}L_m= 2\sum_{\begin{matrix}0\le m\le p\cr m\equiv k~(2)\cr\end{matrix}} {p\choose m}(\alpha^m+\beta^m)=\)
=((\(\displaystyle \alpha\)+1)p+(-1)k(\(\displaystyle \alpha\)-1)p)+((\(\displaystyle \beta\)+1)p+(-1)k(\(\displaystyle \beta\)-1)p)=
=(\(\displaystyle \alpha\)2p+\(\displaystyle \beta\)2p)+(-1)k(\(\displaystyle \alpha\)-p+\(\displaystyle \beta\)-p)=L2p+(-1)k+pLp\(\displaystyle \equiv\)L0=2 (mod Lp).
Az Lp szám páratlan (Ln akkor páros, ha n osztható 3-mal), ezért ebből következik, hogy Lkp\(\displaystyle \equiv\)1 (mod Lp).
A. 331. Bergengócia statisztikai hivatala szerint ha két lakos ismeri egymást, akkor nekik pontosan egy közös ismerősük van, ha nem ismerik egymást, akkor legalább tíz közös ismerősük van.
Lehetséges-e, hogy a statisztikai hivatal információi pontosak?
Megoldás. A válasz: igen, lehetséges. Példát mutatunk tetszőlegesen nagy gráfra, amely teljesíti a feltételeket.
Legyen S egy 3n-elemű halmaz, ahol n\(\displaystyle \ge\)9. A gráfunk pontjai legyenek az S halmaz n-elemű részhalmazai. Két részhalmazt akkor kössünk össze éllel, ha diszjunktak. Megmutatjuk, hogy ez a gráf eleget tesz a feltételeknek.
Tegyük fel, hogy az A és B halmazok össze vannak kötve, azaz diszjunktak. Ekkor egyetlen olyan n-elemű C halmaz van, amely A-val és B-vel is diszjunkt: az \(\displaystyle S\setminus(A\cup B)\) halmaz.
Ha az A és B halmazok nem diszjunktak, azaz nincsenek összekötve, akkor az \(\displaystyle S\setminus(A\cup B)\) halmaz legalább (n+1)-elemű, ezért legalább n+1 olyan n-elemű \(\displaystyle C\subset S\setminus(A\cup B)\) halmaz van, ami A-val és B-vel is diszjunkt.
Megjegyzés. Több versenyző csak a triviális egy-, illetve háromelemű teljes gráfokara mutatott rá. Nekik nem adtunk pontot.

