Exercises and problems in Physics
November 2003

Please read The Conditions of the Problem Solving Competition.

Experimental problem

M. 246. Measure the reflecting power of a glossy black surface as a function of the angle of incidence. Compare this with the reflecting power of a glossy white surface. (6 points)

Theoretical problems It is allowed to send solutions for any number of problems, but final scores of students of grades 9-12 are computed from the 5 best score in each month. Final scores of students of grades 1-8 are computed from the 3 best scores in each month.

P. 3652. Our axe has stuck fast in a clotty log. How can we cleave the log in spite of this? (3 points)

P. 3653. We can heat up a cup of cold cocoa drink by immersing it into hot water up to half-height. Whereas a cup of hot cocoa drink cannot be quickly cooled by cold water the same way. Why? (4 points)

P. 3654. In a mercury thermometer at the temperature of 0 ^oC there is 210 mm³ of mercury, the diameter of the pipe is 0.2 mm. How far are the degree marks on the scale from each other? (4 points)

P. 3655. There is a stick of length \(\displaystyle \ell\) sliding in a horizontal straight tube with a velocity of v₀ without friction and then it slides into another tube where the coefficient of friction is \(\displaystyle \mu\). How long does it take for the stick to slow down and stop? (We can assume that the stick is pressing the tube uniformly.) (5 points)

P. 3656. A small body of mass m hanging on a thread of length \(\displaystyle \ell\) is connected to two horizontal springs of elastic constant D. In the equilibrium position shown in the figure both springs pull the body with a force of F₀ while their length is d. What will the period of the motion be if the body is displaced horizontally by a small distance a) in the plane of the figure? b) perpendicular to the plane of the figure?

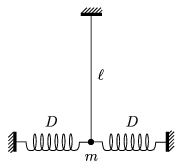
(5 points)

P. 3657. There is a plate capacitor charged up to a voltage of U₀ and then detached from the charger. The distance between the plates is changed periodically: d=d₀+d₁sin \(\displaystyle \omega\)t. How much is d₁ if the voltage of the capacitor changes according to \(\displaystyle U=U_0\left(1+\frac12\sin\omega t\right)\)? (4 points)

P. 3658. How much electric charge goes through resistance R_x if we close switch K? Let a) R_x=0 b) R_x=R.

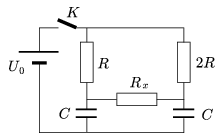
(4 points)

P. 3659. In a thermally insulated tube of a radius of 1 cm there is a liquid of thermal expansion coefficient of 10^-3 K^-1 flowing. Its velocity at the entrance is 0.1 m/s. At the middle of the tube a heater of a power of 10 kW is heating the liquid. The specific heat capacity of the liquid is 1.5 kJ/(kg^.K), and its density is 1500 kg/m³ at the entrance. How much bigger is the volume rate of flow at the end of the tube than at the entrance in cubic meters? (4 points)

P. 3660. How many lines of the Hydrogen spectrum can the human eye see if it can sense the light between wavelengths 380 nm and 760 nm? (3 points)

P. 3661. A square-shaped insulator plate of edge length d is uniformly charged with charge Q. A point-like body of electric charge q is placed on the axis of symmetry of the plate at a d/2 distance from it. What force is exerted on the point charge? (Hint: Compare the force exerted by a small piece of the plate and the flux of charge q crossing this piece of surface.)

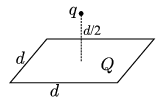
(5 points)

Send your solutions to the following address:

KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary

solutions@komal.elte.hu.

Deadline: 11 December 2003