 |
Exercises and problems in Informatics |
Please read The Conditions of the Problem Solving Competition.
I. 64. The Farey sequence FN for any positive integer N is the sequence of irreducible rational numbers between 0 and 1 for which the denominator is at most N and they are arranged in increasing order. For example, \(\displaystyle F_6=\left\{\frac{0}{1},\, \frac{1}{6},\,\frac{1}{5},\,\frac{1}{4},\,\frac{1}{3},\, \frac{2}{5},\,\frac{1}{2},\,\frac{3}{5},\,\frac{2}{3},\, \frac{3}{4},\,\frac{4}{5},\,\frac{5}{6},\,\frac{1}{1} \right\}.\)
For any given N (1\(\displaystyle \le\)N \(\displaystyle \le\)100), your program (i64.pas, ...) should display the Farey sequence FN.
(10 points)
I. 65. Given N+1 points (xi,yi) in the plane, a Bézier curve nicely approximating them is given by its coordinate-functions x and y in the following parametric form (with 0\(\displaystyle \le\)u \(\displaystyle \le\)1 being a real parameter):
\(\displaystyle x(u)=\sum_{i=0}^nx_i{n\choose i}u^i(1-u)^{n-i},\quad y(u)=\sum_{i=0}^ny_i{n\choose i}u^i(1-u)^{n-i}. \)
Write your program (i65.pas, ...) which reads the coordinates of the N+1 points then draws them together with the corresponding Bézier curve.
Example.:
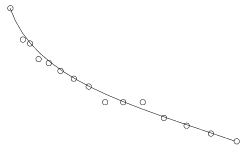
N=14
(10 points)
I. 66. Euler's number triangle is similar to Pascal's triangle, but instead of the binomial coefficients, it contains the Eulerian numbers E(n,k). For 0\(\displaystyle \le\)n \(\displaystyle \le\)15 and 0\(\displaystyle \le\)k \(\displaystyle \le\)n, E(n,k) is defined as the number of permutations of {1,2,...,n} having exactly k permutation ascents (i.e. having k pairs of adjacent positions in the permutation that are out of order).
Prepare your sheet (i66.xls) that - on entering the value of m (0\(\displaystyle \le\)m\(\displaystyle \le\)15) into cell <<\texttt>>A1 - displays the Eulerian numbers E(n,k) (n=0,1,...,m) in the first n+1 rows of the sheet. Numbers should only appear in valid cells.
Example for m=10:
|
