A 2004. januári B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3692.Két dobozban kavicsok vannak, az egyikben p, a másikban q darab. Egy lépésben vagy mindkét dobozból elvehetünk egy-egy kavicsot, vagy pedig az egyik doboz tartalmát megháromszorozhatjuk. Elérhető-e ilyen lépések alkalmas sorozatával, hogy mindkét doboz kiürüljön, ha

a) p=100, q=200;

b) p=101, q=200?

(4 pont)

Megoldás: Ha a két dobozban egy adott pillanatban együttesen páratlan sok kavics van, akkor a következő lépés után is így lesz, hiszen a két dobozban együttesen található kavicsok száma vagy 2-vel csökken, vagy valamelyik dobozban lévő kavicsok számának kétszeresével növekszik: mindenképpen páratlan marad. A b) esetben tehát biztosan nem érhető el, hogy mindkét doboz kiürüljön. A két dobozban bármelyik lépés után összesen páratlan sok kavics lesz, ami legalább egy kavicsot jelent.

Az a) esetben ez a probléma nem merül fel, és ekkor könnyen mutathatunk is egy olyan stratégiát, amelyet alkalmazva mindkét doboz kiürül. Végezzünk el egymás után 50 olyan lépést melynek során mindkét dobozból eltávolítunk egy-egy kavicsot. Ekkor az első dobozban 50, a másodikban 150 kavics lesz. Ezután az első dobozban lévő kavicsok számát megháromszorozva (ehhez még éppen elég kavics áll rendelkezésünkre) elérjük, hogy mindkét dobozban azonos számú (150) kavics legyen. Az egyes dobozokban a kavicsok számát minden egyes további lépesben eggyel csökkentve, 150 újabb lépés után célunkat elérjük.

B.3693.A pozitív egész k számot a p prímszámmal osztva a maradék 6. Ugyanennyi maradékot kapunk akkor is, ha az 1000-k számot osztjuk p-vel; tudjuk ezenkívül, hogy 10 000-k osztható p-vel. Melyik ez a p prímszám?

(3 pont)

Javasolta: Bakonyi Gábor, Budapest

Megoldás: Ha k-6 és (1000-k)-6 is osztható p-vel, akkor összegük, 988=4^.13^.19 is osztható p-vel. Mivel p$\displaystyle \ge$7, p értéke csak 13 vagy 19 lehet. Tudjuk, hogy (k-6)+(10000-k)=9994 is osztható p-vel. Mivel 9994 13-mal osztva 10 maradékot ad, 19-cel viszont osztható, a megoldás csak p=19 lehet. Megjegyezhetjük, hogy ilyen k szám valóban létezik is, például k=25 esetén p=19-cel mindhárom feltétel teljesül.

B.3694.Adott az ABCD konvex négyszög. Szerkesszük meg azt a négy, A csúcson átmenő egyenest, amelyek a négyszöget öt egyenlő területű részre osztják.

(3 pont)

Megoldás: Jelölje a B csúcs AC átlóra eső merőleges vetületét M, a D csúcsét edig N. A négyszög területét t-vel, az ABC és ADC háromszögekét pedig rendre t₁, t₂-vel jelölve t=t₁+t₂, és t₁:t₂=BM:DN. Innen t:t₁=(MB+DN):BM, ahonnan

$\displaystyle \alpha={t/5\over t_1}={BM+DN\over5BM}.$

Hasonlóképpen kapjuk, hogy

$\displaystyle \beta={t/5\over t_2}={BM+DN\over5DN},$

vagyis t/5=$\displaystyle \alpha$t₁=$\displaystyle \beta$t₂. Mivel 1/$\displaystyle \alpha$+1/$\displaystyle \beta$=5, $\displaystyle \alpha$ és $\displaystyle \beta$ közül legalább az egyik 1-nél kisebb. Az általánosság megszorítása nélkül feltehetjük, hogy t₁$\displaystyle \ge$t₂, vagyis $\displaystyle \alpha$<1, sőt $\displaystyle \alpha$<1/2 is teljesül. Ha most X₁ a BC oldal azon pontja, amelyre BX₁:BC=$\displaystyle \alpha$, akkor az ABX₁ háromszög területe $\displaystyle \alpha$t₁=t/5. BX₁:BC=(BM+DN):5BM miatt a párhuzamos szelők tételét alkalmazva BX₁ könnyen megszerkeszthető. Ha ezután a BC oldalon azt az X₂ pontot is kijelöljük, amelyre X₁X₂=BX₁, akkor az AX₁X₂ háromszög területe is t/5 lesz. Ha BC$\displaystyle \ge$3BX₁, akkor ugyanezzel a módszerrel még egy X₃, sőt BC$\displaystyle \ge$4BX₁ esetén egy további X₄ pontot is kijelölhetünk a BC oldalon úgy, hogy BX₁=X₂X₃(=X₃X₄) legyen, ekkor az AX₂X₃ (és AX₃X₄) háromszög területe is t/5 lesz. BC$\displaystyle \ge$4BX₁ esetén már készen is vagyunk, ellenkező esetben $\displaystyle \alpha$>1/4, $\displaystyle \beta$<1, és ekkor az X₄ pontot a DC oldalon szerkesztjük meg, X₁-hez teljesen analóg módon úgy, hogy DX₄:DC=$\displaystyle \beta$ teljesüljön, ami garantálja, hogy a DCX₄ háromszög területe t/5 legyen. Ha BC$\displaystyle \ge$3BX₁, vagyis X₃ szerkesztésére korábban sor került, akkor megint csak készen vagyunk, ellenkező esetben $\displaystyle \alpha$>1/3, $\displaystyle \beta$<1/2, és ekkor az X₃ pontot úgy kell felvennünk a DC szakaszon, hogy X₃X₄=X₄D teljesüljön. Bármelyik eset következzen is be, végeredményben az AX_i egyenesek (1$\displaystyle \le$i$\displaystyle \le$4) a négyszög területét éppen 5 egyenlő részre fogják osztani.

B.3695.Legyen az n pozitív egész szám. Igazoljuk, hogy 5ⁿ-8n²+4n-1 osztható 64-gyel.

(3 pont)

Megoldás: Az a_n=5ⁿ-8n²+4n-1 sorozat első eleme, a₁=0. Mivel ez osztható 64-gyel, a teljes indukció elve szerint elég megmutatni, hogy minden n pozitív egész számra

a_n+1-a_n=5ⁿ⁺¹-8(n+1)²+4(n+1)-1-(5ⁿ-8n²+4n-1)=4(5ⁿ-4n-1)

osztható 64-gyel. Elegendő tehát a b_n=5ⁿ-4n-1 sorozatról megmutatnunk, hogy minden eleme osztható 16-tal. Lévén b₁=0, ehhez csak azt kell látni, hogy minden n pozitív egész számra

b_n+1-b_n=5ⁿ⁺¹-4(n+1)-1-(5ⁿ-4n-1)=4(5ⁿ-1)

osztható 16-tal. Ez pedig igaz, hiszen 5ⁿ-1=5ⁿ-1ⁿ osztható 5-1=4-gyel.

B.3696.Adott egy egyenesen néhány nyílt félegyenes; ezek végpontjai az egyenest részekre osztják. Igazoljuk, hogy a pontosan q számú félegyenes által lefedett részek száma legfeljebb q+1.

(4 pont)

Megoldás: Az egyszerűség kedvéért azonosítsuk az egyenest a számegyenessel. Tekintsünk egy, a felbontásban szereplő részt. Ez egy I=]p,r[ mindkét végén nyitott intervallum, ahol p vagy az az egyenes egy olyan pontja, amely valamely adott félegyenes kezdőpontja, vagy pedig p=-$\displaystyle \infty$. Hasonlóképpen r vagy az egyenes egy olyan pontja, amely valamely adott félegyenes kezdőpontja, vagy pedig r=$\displaystyle \infty$; mindenesetre p<r. Ha I-t pontosan q számú félegyenes fedi le, rendeljünk hozzá I-hez egy nemnegatív egészekből álló (a,b) számpárt, ahol a$\displaystyle \le$q azon ]u,$\displaystyle \infty$[ típusú félegyenesek száma, amelyek I-t tartalmazzák (vagyis amelyekre u$\displaystyle \le$p), b$\displaystyle \le$q pedig azon ]-$\displaystyle \infty$,v[ típusú félegyenesek száma, amelyek I-t tartalmazzák (vagyis amelyekre r$\displaystyle \le$v). Mivel nyilván a+b=q, a pontosan q-szor lefedett részekhez rendelt számpárok a (0,q), (1,q-1),...,(q,0) számpárok közül kerülnek ki. Ez összesen q+1 lehetséges számpár.

Legyen most I=]p,r[ és J=]s,t[ két különböző, a félegyenesek által pontosan q-szor lefedett rész. Feltehetjük, hogy r$\displaystyle \le$s, ekkor nyilván -$\displaystyle \infty$<r$\displaystyle \le$s<$\displaystyle \infty$. Tegyük fel, hogy I-hez és J-hez ugyanazt az (a,b) párt rendeltük hozzá. Legyen f egy olyan félegyenes (az adottak közül) amelynek kezdőpontja r. Ha f=]-$\displaystyle \infty$,r[, akkor az I részt egyrészt lefedi b számú olyan ]-$\displaystyle \infty$, v[ alakú félegyenes, ahol r$\displaystyle \le$s<t$\displaystyle \le$v<$\displaystyle \infty$, és még f is, ami azt jelentené, hogy az I-hez rendelt számpár második tagja b-nél nagyobb. Ez tehát nem lehetséges. Ha pedig f=]r,$\displaystyle \infty$[, akkor a J részt egyrészt lefedi a számú olyan ]u,$\displaystyle \infty$[ alakú félegyenes, ahol -$\displaystyle \infty$<u$\displaystyle \le$p<r, másrészt f is, ami azt jelentené, hogy a J-hez rendelt számpár első tagja a-nál nagyobb, ami szintén nem lehetséges. Ennélfogva bármely két különböző, pontosan q-szor fedett részhez más-más számpárt rendeltünk hozzá a q+1 lehetséges számpár közül, amiből az állítás azonnal következik.

B.3697.Oldjuk meg a következő egyenletet: $\displaystyle x^2+ \left(\frac{5x}{x-5}\right)^{\!\!2}=11$.

(4 pont)

Megoldás: Feltesszük, hogy x$\displaystyle \ne$5, ekkor ugyanis a baloldalon álló tört nem értelmezhető. Ebben az esetben az egyenlet ekvivalens az x²(x-5)²+(5x)²=11(x-5)² egyenlettel. Rendezés után a következő negyedfokú egyenletet kapjuk:

x⁴-10x³+39x²+110x-275=0.

A baloldalt szorzattá alakítva

(x²-11x+55)(x²+x-5)=0,

ahonnan x²-11x+55=0 vagy x²+x-5=0. Az első eset nem lehetséges, hiszen az egyenlet diszkriminánsa, 11²-4^.55 negatív. Tehát x²+x-5=0, ahonnan

$\displaystyle x={-1\pm\sqrt{21}\over2}$

az eredeti egyenlet két megoldása, hiszen ezek az x$\displaystyle \ne$5 feltételt is kielégítik.

B.3698.Szerkesszünk négyszöget, ha adottak az oldalaira kifelé írt szabályos háromszögeknek a négyszög csúcsaitól különböző csúcsai. A szerkeszthetőség feltételeinek vizsgálatától ezúttal eltekintünk.

(5 pont)

Megoldás: A szerkesztendő négyszög csúcsait pozitív forgásirányban jelölje rendre A,B,C, D, az XY oldalra kifelé írt szabályos háromszög X,Y-tól különböző csúcsát pedig jelöljük P_XY-nal. Legyen ezen kívül X' az ABCD négyszög X csúcsának az X csúcsot nem tartalmazó átló felezőpontjára vonatkozó tükörképe. A P_ABA szakaszt a P_AB pont körül negatív irányban 60^o-os szöggel elforgatva kapjuk a P_ABB szakaszt, az AP_AD szakaszt az A pont körül negatív irányban 60^o-os szöggel elforgatva pedig az AD szakaszhoz jutunk. Mivel $\displaystyle \overrightarrow{AD}=\overrightarrow{BA'}$, látható, hogy a P_ABAP_AD háromszöget a P_AB pont körül negatív irányban 60^o-os szöggel elforgatva éppen a P_ABBA' háromszöghöz jutunk. Az A' pontot tehát megkapjuk, ha a P_ABP_AD szakaszt elforgatjuk a P_AB pont körül negatív irányban 60^o-os szöggel. Ugyanígy a D' pont is meghatározható, ha a P_ADP_CD szakaszt forgatjuk el a P_AD pont körül negatív irányban 60^o-os szöggel. Az A'D' szakasz felezőpontja a BC oldal F_BC felezőpontja is egyben. Az F_BC és P_BC pontok pedig a B,C pontok helyét egyértelműen meghatározzák: a B pont megkapható, ha a P_BCF_BC félegyenest elforgatjuk P_BC körül pozitív irányban 30^o-kal, és kijelöljük ennek a félegyenesnek a P_BCF_BC szakaszra annak F_BC végpontjában állított merőlegessel alkotott metszéspontját; C pedig a B pont tükörképe az F_BC pontra.

Tegyük fel tehát, hogy az adott pontokhoz létezik megfelelő négyszög. A négy pont valamilyen sorrendben a P_AB,P_BC,P_CD és P_AD pontoknak fog megfelelni. Rögzítsünk egyet a 24 lehetséges sorrend közül. (Igazából elég 6 különböző sorrendet megvizsgálni, hiszen az A,B,C,D csúcsok egy ciklikus permutációjának a P_AB,P_BC,P_CD,P_AD ugyanolyan ciklikus permutációja felel meg.) A fent említett észrevételek alapján először alkalmas 60^o-os elforgatásokkal megszerkeszthetjük az A',D' pontokat, majd az F_BC pont kijelölése után a B és C pontokat. Ugyanilyen eljárással az A és D csúcsok is megszerkeszthetők. Ha a kapott A,B,C,D pontok nem alkotnak pozitív körüljárású négyszöget, akkor az adott pontok egy újabb sorrendjével megismételjük a szerkesztési eljárást, egészen addig, amíg végül egy megfelelő négyszöget kapunk.

B.3699.Az egységsugarú kör AB átmérőjén adott a P pont. A P ponton átmenő szelő a C és D pontokban metszi a kört. Milyen nagy lehet az ABCD négyszög területe?

(5 pont)

Megoldás: Vegyünk fel úgy egy derékszögű koordinátarendszert, hogy a kör középpontja az origóba essen, a P pont koordinátái pedig 0 és d legyenek, ahol 0$\displaystyle \le$d<1. Ha d=0, akkor a megoldás nyilvánvaló, a legnagyobb területű négyszöget az AB-re merőleges CD szelő fogja szolgáltatni, ekkor az ABCD négyszög egy 2 egység területű négyzet lesz. A továbbiakban feltesszük, hogy d>0. A szelő egyenlete y=mx+d alakú, ahol m$\displaystyle \ge$0 feltehető (m<0 esetén csak az x tengely irányítását kell megváltoztatnunk). Ha a szelő a C(x₁,y₁) és D(x₂,y₂) pontokban metszi a kört, akkor lévén AB a kör y tengelyre eső átmérője, az ABCD négyszög területe éppen T=|x₁|+|x₂|. Mivel y_i=mx_i+d és x_i²+y_i²=1,

(m²+1)x_i²+2mdx_i+(d²-1)=0,

ahonnan

$\displaystyle x_{1,2}={-md\pm\sqrt{(md)^2+(1-d^2)(m^2+1)}\over m^2+1}.$

Mivel 1-d²>0, a gyökös kifejezés értéke nagyobb, mint md$\displaystyle \ge$0, ezért

$\displaystyle T=|x_1|+|x_2|=2{\sqrt{(md)^2+(1-d^2)(m^2+1)}\over m^2+1},$

vagyis az y=m²+1$\displaystyle \ge$1 helyettesítés után

$\displaystyle {T^2\over4}={(y-1)d^2+(1-d^2)y\over y^2}={y-d^2\over y^2}.$

Jelöljük ezt az értéket $\displaystyle \alpha$-val, és keressük meg $\displaystyle \alpha$ lehető legnagyobb értékét d függvényében. Mivel most $\displaystyle \alpha$y²-y+d²=0, d$\displaystyle \ne$0 miatt egyenlőségünket

$\displaystyle \Bigl(d-{y\over2d}\Bigr)^2=\Bigl({1\over4d^2}-\alpha\Bigr)y^2$

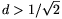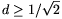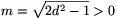alakba írhatjuk. Innen rögtön látszik, hogy $\displaystyle \alpha$ $\le$ 1/4d². Ha most $d>1/\sqrt{2}$ akkor $\alpha$ =1/4d² esetén az y=2d² megoldást kapjuk, amire y> 1 is teljesül. Ha tehát $d\ge1/\sqrt{2}$ akkor $m=\sqrt{2d^2-1}>0$ esetén kapjuk a lehetséges legnagyobb területű négyszöget, melynek területe 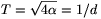$T=\sqrt{4\alpha}=1/d$ lesz. Ez az út nem járható, ha 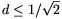$d\le1/\sqrt{2}$ . Ekkor így okoskodhatunk. Világos, hogy $\alpha$ =1-d² esetén y=1 megoldása az egyenletnek, y>1 esetén pedig z=y-1>0 helyettesítéssel

(1-d²)y²-y+d²=(1-d²)z²+(1-2d²)z $\ge$ (1-d²)z²>0,

más megoldás tehát nem lehetséges. Ha viszont $\alpha$ >1-d², akkor

$\alpha$ y²-y+d²>(1-d²)y²-y+d² $\ge$ (1-d²)z² $\ge$ 0,

így most egyáltalán nem kaphatunk megoldást. Ebben az esetben tehát a legnagyobb területű négyszöget y=1, m=0 esetén kapjuk, a négyszög területe ekkor 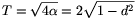$T=\sqrt{4\alpha}=2\sqrt{1-d^2}$ .

Összefoglalva, ha a P pont a kör középpontjától 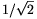$1/\sqrt{2}$ -nél nagyobb d távolságra esik, akkor az ABCD négyszög lehetséges legnagyobb területe 1/d, és ezt csak két, az AB egyenesre szimmetrikusan elhelyezkedő szelő segítségével érhetjük el. 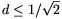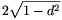Ha a P pont a kör középpontjától $d\le1/\sqrt{2}$ távolságra esik, akkor egyetlen maximális területű négyszög létezik, melyet az AB átmérőre merőleges szelő szolgáltat; a négyszög területe ekkor $2\sqrt{1-d^2}$ .

B.3700.Bizonyítsuk be, hogy az x₁,x₂,...,x_n pozitív számokra

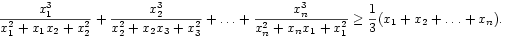
$\frac{x_1^3}{x_1^2+x_1x_2+x_2^2}+ \frac{x_2^3}{x_2^2+x_2x_3+x_3^2}+\ldots+ \frac{x_n^3}{x_n^2+x_nx_1+x_1^2}\ge\frac{1}{3}(x_1+x_2+\ldots+ x_n).$

(5 pont)

Gillis-Turán verseny

Megoldás: Jelöljük a baloldalon álló kifejezést S-sel, és legyen

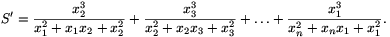
$S'={x_2^3\over x_1^2+x_1x_2+x_2^2}+{x_3^3\over x_2^2+x_2x_3+x_3^2}+\ldots+ {x_1^3\over x_n^2+x_nx_1+x_1^2}.$

Ekkor

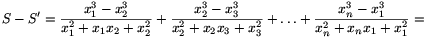
$S-S'={x_1^3-x_2^3\over x_1^2+x_1x_2+x_2^2}+ {x_2^3-x_3^3\over x_2^2+x_2x_3+x_3^2}+\ldots+ {x_n^3-x_1^3\over x_n^2+x_nx_1+x_1^2}=$

=(x₁-x₂)+(x₂-x₃)+...+(x_n-x₁)=0.

Ezek szerint S=S', és ezért elég annyit bizonyítani, hogy

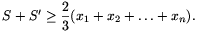
$S+S'\ge{2\over3}(x_1+x_2+\ldots+x_n).$

Ehhez pedig nyilván elegendő igazolni az

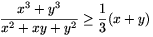
${x^3+y^3\over x^2+xy+y^2}\ge{1\over3}(x+y)$

egyenlőtlenséget, ahol x,y pozitív számok. Ez azonban ekvivalens a 3(x³+y³) $\ge$ (x²+xy+y²)(x+y), a pozitív (x+y) kifejezéssel történő leosztás után pedig a 3(x²-xy+y²) $\ge$ x²+xy+y² egyenlőtlenséggel. Rendezve a 2(x-y)² $\ge$ 0 egyenlőtlenséghez jutunk. Ez nyilván mindig teljesül; egyenlőség pedig pontosan az x=y esetben áll fenn. Ha az eredeti egyenlőtlenségben a két oldal egyenlő, akkor szükségképpen minden 1 $\le$ i <n esetén

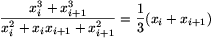
${x_i^3+x_{i+1}^3\over x_i^2+x_ix_{i+1}+x_{i+1}^2}= {1\over3}(x_{i}+x_{i+1})$

kell, hogy teljesüljön, ahonnan x₁=x₂=...=x_n. Ebben az esetben pedig az egyenlőtlenség mindkét oldalán a közös x_i érték n/3-szorosa áll.

B.3701.Legyen P egy kocka tetszőleges belső pontja. Mutassuk meg, hogy legalább hat olyan tetraéder van, melynek minden csúcsa a kockának is csúcsa, továbbá tartalmazza a P pontot.

(4 pont)

Megoldás: Az alábbiakban megadjuk a kocka 6 különböző felbontását tetraéderekre úgy, hogy a 6 felbontásban szereplő tetraéderek minden csúcsa egyben a K kockának is csúcsa, és ezen tetraéderek mind különböznek egymástól. Ebből az állítás már azonnal következik.

Két felbontást kaphatunk a következő módon. Tekintsük a kocka 4 pároként másodszomszédos csúcsát, ezek egy olyan T tetraédert határoznak meg, melynek térfogata K térfogatának egyharmada. T eltávolításával a kocka 4 további egymásba nem nyúló tetraéderre esik szét, melyek mindegyike pontosan illeszkedik K egy jól meghatározott sarkába. Mivel T két részre vágja mind a négy testátlót, sem T-nek, sem a másik 4 tetraédernek nem lehet éle egyik testátló sem. Jelöljük ezt a felbontást 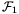${\cal F}_1$ -gyel. Egy másik hasonló tulajdonságokkal bíró 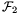${\cal F}_2$ felbontást kaphatunk olyan módon, hogy a 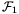${\cal F}_1$ -ben szereplő 5 tetraédert tükrözzük K középpontjára. A két felbontásban szereplő 10 tetraéder mind különböző, hiszen T és annak tükörképe nagyobb térfogattal rendelkezik, mint a többi, a maradék 8 tetraéder pedig rendre a kocka 8 különböző sarkába illeszkedik pontosan.

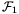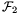A hátralévő 4 felbontást úgy fogjuk megcsinálni, hogy az azonos felbontásban szereplő tetraéderek mindegyikének lesz egy olyan éle, amely megegyezik a kocka valamelyik testátlójával. Ebből következik, hogy ezen tetraéderek egyike sem egyezhet meg ${\cal F}_1$ vagy ${\cal F}_2$ -beli tetraéderrel. Egymás közt pedig azért lesznek mind különbözők, mert az ugyanabban a felbontásban szereplő tetraédereknek közös élük lesz K egy testátlója, amely testátló más és más lesz a 4 felbontás mindegyikében. Mivel K-nak pontosan 4 testátlója van, elég kiválasztani az egyik t testátlót, és mutatni K egy olyan felbontását megfelelő tetraéderekre, melyben minden egyes tetraédernek t lesz az egyik éle. Ha most t=AB, akkor tekintsük a kockának azt a 3 lapját, amelynek a B pont csúcsa, és mindhárom lapot osszuk fel két háromszögre úgy, hogy a B pont a két háromszög közös csúcsa legyen. A keletkezett 6 háromszög mindegyikét az A csúccsal összekötve 6 tetraédert kapunk, melyek K-nak egy megfelelő felbontását szolgáltatják.

Már regisztráltál?
Új vendég vagy?