Exercises and problems in Physics
February 2004

Please read The Conditions of the Problem Solving Competition.

Experimental problem

M. 250. Measure the torsion constant of a single hair. Take more measurements in different air-humidity conditions and examine the damping of the oscillations as well.

(6 points)

Theoretical problems It is allowed to send solutions for any number of problems, but final scores of students of grades 9-12 are computed from the 5 best score in each month. Final scores of students of grades 1-8 are computed from the 3 best scores in each month.

P. 3692. A group of children are riding home on a bus. The balloons in the hands of some kids are hanging already while in the hands of others they are still about to lift. Suddenly the bus brakes. Which way are the balloons going to move?

(3 points)

P. 3693. Swimming-spider and Wonder-spider are waiting on a table for their prey at a 20 cm distance from each other. Suddenly they see a small caterpillar and at once they both cast their threads. At this moment the caterpillar is 20 cm away from Swimming-spider and 30 cm away from Wonder-spider. The hungry spiders pull the ends of their threads with a velocity of \(\displaystyle 1~\frac{\rm cm}{\rm s}\) while they keep their positions. The threads do not change their lengths and are tight all the way. When is the caterpillar between the two spiders? What is its path like?

(4 points)

P. 3694. We stick a Scotch-tape (adhesive tape) on a tabletop. We grab one end of it and pull it back horizontally and uniformly with a velocity of 10 cm/s. What is the velocity of the middle of the moving part of the tape?

(4 points)

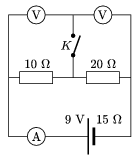
P. 3695. In the circuit shown in the figure the electromotive force of the battery is 9 V and its internal resistance is 15 \(\displaystyle \Omega\). The two identical voltmeters and the ammeter can all be considered ideal. What do the instruments show when switch K is open and when it is closed?

(4 points)

P. 3696. The primary coil of a transformer is connected to a power source of a voltage of 230 V. In the unknown resistance connected to the secondary coil a current of 0.2 A can be measured. If the two coils are interchanged the current measured is 1.8 A. What is the unknown resistance? What is the ratio of the number of turns of the two coils?

(4 points)

P. 3697. A pebble is thrown horizontally from the top of a 60 m high tower with an initial velocity of 20 m/s. The air drag is negligible. What is the velocity of the pebble when it is at the same distance from its initial position and the ground?

(4 points)

P. 3698. From a plastic cylinder of radius R a cylinder-shaped part of radius R/2 is cut out. The axes of the cylinder cut out and the original cylinder are parallel and their distance is d. The resultant hollow cylinder is put on a slope with its axis horizontal. At what slope angle can the hollow cylinder stand in a state of stable equilibrium on the slope? (The friction is adequately large.)

(5 points)

P. 3699. One end of the L=1.2 m long homogeneous rod of mass m=10 kg, shown in the figure, is fixed to a hinge. A cylindrical spring of spring constant D=200 N/m fixed to its other end keeps it in equilibrium exactly horizontally. What is the elastic energy stored in the spring? Making the system oscillate vertically with a small displacement, what will its period be?

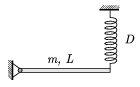
(5 points)

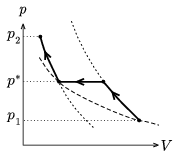
P. 3700. In a vessel closed by a piston air is compressed from pressure p₁ to pressure p₂. The compression is adiabatic first then at a certain pressure p^* the process becomes isobar. When the gas cools down to its original temperature the compression continues, again adiabatically. At what value of p^* is the work done during compression the smallest?

(5 points)

P. 3701. 0.9 g of water is dropped into a vessel of a volume of 5 l at a temperature of 0 ^oC and pressure of 1.013^.10⁵ Pa. Then the vessel is sealed. What is the pressure in the vessel at a temperature of 35 ^oC? At what temperature does all the water evaporate, and what is the pressure in the vessel in this case?

(5 points)

Send your solutions to the following address:

KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary

solutions@komal.elte.hu.

Deadline: 11 March 2004