Exercises and problems in Physics
April 2004

Please read The Conditions of the Problem Solving Competition.

Experimental problem

M. 251. In what way does resistance to rolling at the wheel of a bicycle depend on the air pressure in the tyres?

(6 points)

Theoretical problems It is allowed to send solutions for any number of problems, but final scores of students of grades 9-12 are computed from the 5 best score in each month. Final scores of students of grades 1-8 are computed from the 3 best scores in each month.

P. 3702. A glass of a height of 4 cm and of a diameter of 3 cm is lying tumbled over in the horizontal kitchen sink. The water level in the sink is such that, if we raised it by 25%, it would just cover the glass lying on its side. (The wall thickness of the glass is negligible.) If we stood the glass up slowly, in a way that it always touches the bottom of the sink, what would the water level be in the glass in the end? Would it rise from the bottom, if we released it?

(4 points)

P. 3703. All the bulbs drawn on the connection diagram shown in the figure radiate with the same brightness (effective power). The resistance of Bulb 1 is 36 ohm. a) What are the resistances of the other bulbs? b) How will the brightness of each individual bulb change if we connect point C first with point X and then with point Y using a flexible wire? c) What is the output voltage of the battery, if the power of each bulb is equally 4 W (before connecting)?

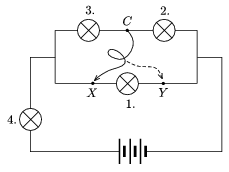
(4 points)

P. 3704. The length of both sections AB and EF is l₁ in the figure, and their coefficient of thermal expansion is \(\displaystyle \alpha\)₁. The length of section CD is l₂ and its expansion coefficient is \(\displaystyle \alpha\)₂. What must the ratio l₁/l₂ be to ensure that distance AF remains the same at all temperatures? (Points A, B, E and F reside on the same line.)

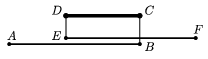
(3 points)

P. 3705. A table-tennis ball made by gluing together its two hemispheres and filled with water is hung in a way that the gluing line (which, for the sake of simplicity, is considered a single circular line) is in a horizontal plane. A small air bubble is left at the top of the water at the atmospheric pressure. The thread it is hung on is pulled by a force of F₀. What load (force) the gluing line is to cope with?

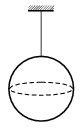
(5 points)

P. 3706. The volume of water vapor of a temperature of 100 ^oC and a pressure of 50 Pa is beginning to decrease at constant temperature. What is the pressure of the vapor when its volume is one fourth of the original?

(4 points)

P. 3707. Two electric point charges, Q₁ and Q₂ are both fixed on a long, horizontal insulator thread. Where on the thread is it possible for a tiny bead of electric charge Q₃ to be in the state of equilibrium in the electric field generated by point charges Q₁ and Q₂, and what kind of equilibrium is it?

(4 points)

P. 3708. A plate capacitor of plate distance d is charged up to a voltage of 500 V. We push another plate capacitor of the same size and same voltage of a plate distance of \(\displaystyle \frac{3}{5}d\) between its plates. a) What will the voltage of the capacitor of plate distance d be after the insertion of the other capacitor? b) How many times is the energy of this system bigger than the original energy of the capacitor of plate distance d?

(4 points)

P. 3709. Does the Earth's magnetic field affect the motion of a pendulum made of a metal thread?

(4 points)

P. 3710. What parent element has an isotope with a nucleus containing 120 neutrons, and having an electric charge density of 5.34 PC/mm³?

(4 points)

P. 3711. The graph shows the magnitude of the velocity of a body moving on a slope measured by an instrument (V-scope) as a function of time. At the bottom of the slope there was a bumper. With the help of the graph determine a) the angle of the slope and the friction coefficient, b) the average force acting in the second collision, c) the mechanical loss in the third collision. The mass of the body moving on the slope is 100 g, the instrument measures the velocity every 30 ms.

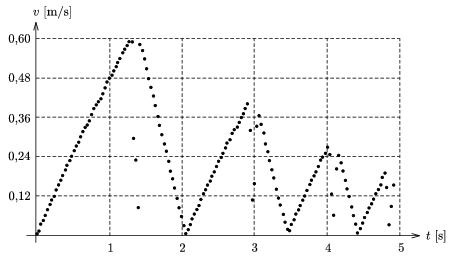
(5 points)

Send your solutions to the following address:

KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary

solutions@komal.elte.hu.

Deadline: 11 May 2004