 |
Exercises and problems in Informatics |
Please read The Conditions of the Problem Solving Competition.
I. 76. Write a program (i76.pas, ...) that computes for any positive integer x (1\(\displaystyle \le\)x \(\displaystyle \le\)500000) the number of ordered positive integer pairs [a,b] such that the least common multiple of a and b is x.
Example. For x=3 the output should be 3, since the appropriate pairs are [1,3], [3,3] and [3,1], while for x=6 the answer is 9, since the pairs now are [1,6], [2,3], [2,6], [3,6], [6,6], [6,3], [6,2], [3,2], [6,1]. (10 points)
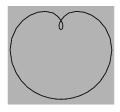
I. 77. Interesting figures are obtained if the sine function is composed with power functions using the following formula: ra=sin (a\(\displaystyle \varphi\)), where a is a real parameter, and r and \(\displaystyle \varphi\) represent the points of the curve in the usual polar-coordinates.
Write your program (i77.pas, ...) which plots such a curve for any given value of a. The example shows the curve corresponding to \(\displaystyle a=\frac{1}{2}\). (10 points)
I. 78. Ackermann studied computability and complexity of functions. The so-called Ackermann function of two nonnegative integer arguments is recursively defined by
\(\displaystyle A(n,m)=\begin{cases} m+1,&\mbox{if\ }n=0\\ A(n-1,1),&\mbox{if\ }\)0,\ m=0\\ A\big(n-1,A(n,m-1)\big),&\mbox{if\ }n>0,\ m>0. \end{cases} ">
An interesting property of this function is that it grows faster than any other ``ordinary'' function, further, explicit representation of A(n,m) is known only for very special values of n and m.
Prepare a sheet (i78.xls) that computes the values of the Ackermann function in the following form (the message #REF! (or #HIV!) can appear if we are no longer able to compute the actual value). (10 points)
|
