A 2004. májusi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C.765.Egy kihúzható kerek asztal átmérője 1 méter. Kihúzott állapotban az asztallap két félkör alakú része közé egy 1 m x0,5 m-es téglalap illeszkedik. Van-e ekkor az asztallapnak két, egymástól 150 cm-nél távolabb lévő pontja?

Megoldás:

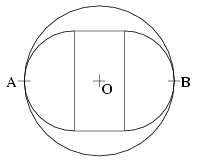
Az O középpontú, $\displaystyle {150\over2}$ sugarú kör tartalmazza az asztal lapját. Egy körben a legnagyobb távolság az átmérő, ez jelen esetben 150 cm. Így az asztallapon is legfeljebb ekkora a legnagyobb távolság, ez A és B esetében létre is jön.

C.766.A konyhában lévő falióra naponta 2 másodpercet késik, a szobában lévő antik óra naponta 15 másodpercet siet. Vasárnap délben a falióra 12 óra 1 percet, az antik óra 11 óra 59 percet mutat. Mikor lesz a hét folyamán az órák által mutatott és a valódi idő közötti különbségek négyzetösszege a legkisebb?

Megoldás: n nappal vasárnap dél után a valódi időtől való eltérés a falióra esetében 60-2n, az antik óra esetében pedig 15-60n. Tehát (60-2n)²+(15n-60)² minimumhelyét keressük.

$\displaystyle (60-2n)^2+(15n-60)^2=229n^2-2040n+7200=229\left(n^2-{2040\over229}n+{7200\over229}\right)=$

$\displaystyle =229\left[\left(n-{1020\over229}\right)^2-\left({1020\over229}\right)^2+{7200\over229}\right]$

minimális, ha

$\displaystyle n={1020\over229}=4{104\over229}\approx4{39238\over86400}=4{10\cdot3600+53\cdot60+58\over86400},$

vagyis csütörtökön, körülbelül 22 óra 53 perc 58 másodperckor.

C.767.Határozzuk meg az összes olyan nem negatív a, b, c számot, amelyre: $\displaystyle \sqrt{a-b+c}=\sqrt{a}-\sqrt{b}+\sqrt{c}$.

Megoldás:

$\displaystyle \sqrt{a-b+c}=\sqrt a-\sqrt b+\sqrt c$

$\displaystyle \sqrt{a-b+c}+\sqrt b=\sqrt a+\sqrt c$

Ebből négyzetre emelés és rendezés után

$\displaystyle \sqrt{ab-b^2+bc}=\sqrt{ac}$

adódik. Ismét négyzetre emelve, majd rendezve

(a-b)(b-c)=0.

Ebből a=b$\displaystyle \ge$0, c$\displaystyle \ge$0 tetszőleges vagy b=c$\displaystyle \ge$0, a$\displaystyle \ge$0 tetszőleges; mindkét esetben az eredeti egyenletet is kielégítő megoldásokat kapunk.

C.768.Két egységnyi sugarú kör az A és B pontokban metszi egymást. Egyik közös érintőjük az E és F pontokban érinti a köröket. Mekkora lehet annak a körnek a sugara, amelyik áthalad az E, F és A pontokon?

Megoldás:

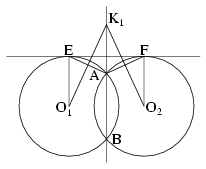
AF és AE felezőmerőlegese a K₁ pontban metszi egymást az ábrán látható módon. A kapott négy háromszög egybevágó, vagyis K₁A=O₂F=1. Ha a B-hez közelebbi érintőt vesszük, akkor hasonló módon szintén r=1 adódik.

C.769.Egy 20 cm sugarú henger az e egyenes mentén érinti a sík talajt. Az e egyenesre merőlegesen egy 50 cm hosszú pálcát támasztunk a hengernek úgy, hogy a pálca talajon lévő végpontja 40 cm-re van az e egyenestől. Milyen magasan van a pálca másik végpontja?

Megoldás:

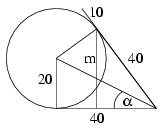
$\displaystyle {m\over40}=\sin2\alpha=2\sin\alpha\cos\alpha=2\cdot{20\over20\sqrt5}\cdot{40\over20\sqrt5}={4\over5}$

m=32

Tehát a pálca másik végpontja $\displaystyle 32\cdot{50\over40}=40$ cm magasan van.