 |
Exercises and problems in Informatics |
Please read The Conditions of the Problem Solving Competition.
I. 79. A Pierce sequence of order N is the monotonic increasing sequence of nonnegative fractions such that each denominator is at most N. (Fractions having the same value in the list are placed in order of decreasing denominators.) Write a program (i79.pas, ...) that computes a Pierce sequence of order N with terms not exceeding M (1\(\displaystyle \le\)M \(\displaystyle \le\)100, 1\(\displaystyle \le\)N \(\displaystyle \le\)100 with integer N).
Example: if N=2 and M=3, then the corresponding Pierce sequence is
\(\displaystyle \frac{0}{2},\ \frac{0}{1},\ \frac{1}{2},\ \frac{2}{2},\ \frac{1}{1},\ \frac{3}{2},\ \frac{4}{2},\ \frac{2}{1},\ \frac{5}{2},\ \frac{6}{2},\ \frac{3}{1}. \)
(10 points)
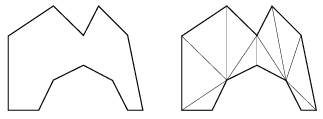
I. 80. Write a program (i80.pas, ...) that reads the coordinates of N vertices of a polygon (3\(\displaystyle \le\)N\(\displaystyle \le\)100 and all coordinates are integers between 0 and 500), then displays a triangulation of the polygon (using any method), see the example with N=12.
(10 points)
I. 81. Prepare a worksheet (i81.xls) that displays Eulerian numbers E(n,k) of the second kind in n+1 rows, if the value of n is written into cell A1.
E(n,k) can be computed in the following way. First take all permutations of the sequence {1,1,2,2,...,n,n} with the property that between the two occurrences of any number m there are no numbers below m. Then E(n,k) is the number of the permutations above containing exactly k increasing subsequences.
| n\k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 1 | ||||||||||
| 1 | 1 | 0 | |||||||||
| 2 | 1 | 2 | 0 | ||||||||
| 3 | 1 | 8 | 6 | 0 | |||||||
| 4 | 1 | 22 | 58 | 24 | 0 | ||||||
| 5 | 1 | 52 | 328 | 444 | 120 | 0 | |||||
| 6 | 1 | 114 | 1452 | 4400 | 3708 | 720 | 0 | ||||
| 7 | 1 | 240 | 5610 | 32120 | 58140 | 33984 | 5040 | 0 |
(10 points)
