New exercises and problems in Mathematics
September
2004
Please read The Rules of the Problem Solving Competition.
 | New exercises for beginnersSolutions can be submitted only by students of grade 9. Maximum score for each exercise (sign "K") is 6 points. |
K. 1. There is a pawn on each of the fields B8 and G8 of a chessboard. What is the minimum number of steps required for a knight on B1 to take both of them if the pawns do not move? (Suggested by Z. Nagy, Hortobágy)
K. 2. In the array of numbers below, we need to move from the field containing the
2 in bold type to the field with the 8 in bold type. We are allowed to traverse each field at most once, and from each field we must move to a neighbouring one having a common edge with it. The numbers in all the fields thus traversed are added. What is the largest possible sum that we can obtain?
K. 3. The vertices of a quadrilateral in the coordinate plane are A(0,0), B(5,0), C(3,2), D(0,1). Show that the diagonals enclose a 45o angle.
K. 4. Determine the (positive) prime numbers p and q, given that p + p2 + p4 - q -q2 - q4 = 83 805.
K. 5. The perpendiculars dropped from the intersection of the angle bisectors of an isosceles triangle onto the sides divide the triangle into three kites: a large one and two smaller ones. For which isosceles triangle will the sum of the areas of the small kites be equal to the area of the larger kite?
K. 6. An island is populated by two kinds of people: the good and the bad. The good always tell the truth while the bad always lie. Each inhabitant of the island is either a man or a woman. Here there are two statements of Ali and Bali, inhabitants of the island about themselves: - Ali: ``We are bad.'' - Bali: ``We are men.'' Determine their character (good or bad) and also their sex. (Suggested by B. Szalkai, Veszprém)
 | New exercisesMaximum score for each exercise (sign "C") is 5 points. |
C. 770. The students in a class can be divided into two groups: beanpoles and brains. Beanpoles claim that they are taller than brains and brains consider themselves better at mathematics. One of them asked a beanpole, ``What do you mean by your being taller than us? Do you mean that - 1. Every beanpole is taller than all the brains? - 2. The tallest beanpole is taller than the tallest brain? - 3. Every beanpole is taller than some brain? - 4. Every brain is shorter than some beanpole? - 5. The shortest brain is shorter than the shortest beanpole?'' The questions visibly made the beanpole shrink... But the task remains to establish the relationship between the above statements. For each pair of statements, decide whether one follows from the other. (Inspired by Hugo Steinhaus)
C. 771. Maths City and Physicstown lie in different time zones. A plane leaves Physicstown at 8 a.m., local time, and arrives in Maths City on the same day at noon, local time. Two hours later it returns, and finally arrives in Physicstown at 8 p.m., local time. The flight takes the same time in each direction. What time is it in Physicstown when it is twelve, noon in Maths City?
C. 772. Once upon a time, in a mathematics class a student got the squaring (a+2b-3)2 wrong and obtained a2+4b2-9. The teacher urged him to check the result by substitution. Substituting natural numbers for a and b, respectively, he found that the result was correct. Which numbers did he substitute?
C. 773. The parallel sides of a trapezoidal plot of land are 2100 and 1500 metres long. The lengths of the other two sides are 613 metres and 37 metres. Find the area of the plot in square yards.
C. 774. Find the area of the figure formed by those points P(x;y) in the coordinate plane for which |x+y|+|x-y|\(\displaystyle \le\)4.
 | New problemsThe maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month. |
B. 3742. The students in a class can be divided into two groups: beanpoles and brains. Beanpoles claim that they are taller than brains and brains consider themselves better at mathematics. One of them asked a beanpole, ``What do you mean by your being taller than us? Do you mean that - 1. Every beanpole is taller than all the brains? - 2. There are more brains shorter than the shortest beanpole than beanpoles shorter than the tallest brain? - 3. The number of beanpoles who are taller than some brains is larger than the number of brains who are taller than some beanpoles? - 4. The average height of brains is smaller than the average height of the beanpoles?'' The questions visibly made the beanpole shrink... But the task remains to establish the relationship between the above statements. For each pair of statements, decide whether one follows from the other. (Inspired by Hugo Steinhaus) (4 points)
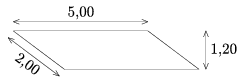
B. 3743. Cut the parallelogram in the Figure into two pieces that can be folded into a cube of unit edge. (Suggested by K. Hajba, Kisvárda) (5 points)
B. 3744. How many positive integers n are there, such that n2+10n is a perfect square? (3 points)
B. 3745. a, b, c, d are numbers for which a+b>|c-d| and c+d>|a-b|. Prove that a+c>|b-d|. (3 points)
B. 3746. The points M and N lie on the side AB of an equilateral triangle ABC,P lies on the side BC and Q lies on the side CA. Given that MA+AQ=NB+BP=AB, determine what angle the lines MP and NQ may enclose. (4 points)
B. 3747. The sides of a triangle are a, b, c and its area is \(\displaystyle \frac{(a+b+c)(a+b-c)}{4}\). Find the largest angle of the triangle. (4 points)
B. 3748. The lines of the altitude and median drawn from the vertex C of a triangle ABC divide the angle BCA into three equal parts. Show that the triangle is right angled. (4 points)
B. 3749. The lengths of the sides of a rectangle are 5 cm and 9 cm. The rectangle is divided into ten smaller rectangles of integer sides (expressed in centimetres). Prove that there are two congruent ones among them. (5 points)
B. 3750. In the sequence {an}, a1 < a2 are positive integers, and ak = 4ak-1-3ak-2 for k\(\displaystyle \ge\)3. Prove that a45 > 343. (4 pont)
B. 3751. Let \(\displaystyle f(x)=\frac{x}{1-x}\). Find the largest subset of the set of real numbers where the composite functions \(\displaystyle f^{(n)}(x)=\underbrace{f \big(f\big(\dots\big(f}_{n}(x)\big)\dots\big)\big)\) are defined for all positive n. (4 points)
 | New advanced problemsMaximum score for each advanced problem (sign "A") is 5 points. |
A. 350. Find all positive integers p, such that the polynomial 4x2+p admits a prime value for each of the numbers 0,1, ...,p-1.
A. 351. Let n\(\displaystyle \ge\)3 and a1, a2, ...,an positive numbers whose sum and product are S and P, respectively. Prove that
\(\displaystyle \sum_{i=1}^n\frac{1}{S-a_i}<\sqrt[n-1]{\frac{S}{P}}. \)
A. 352. Let k be the circumscribed circle of the scalene triangle ABC. Let K denote the intersection of the interior angle bisector at vertex C with the tangent drawn to k at B, and let L be the other common point of the exterior angle bisector at C with the circle k. Let the lines AC and LB intersect at M. Show that the line MK passes through the midpoint of the side AB.
Send your solutions to the following address:
- KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary
