Fizikából kitűzött gyakorlatok és feladatok
2004. október

Kérjük, olvassa el a versenykiírást.

Mérési feladat

M. 254. Mérjük meg egy száraz és egy teljesen átázott hurkapálca sűrűségét! Vizsgáljuk meg azt is, hogyan változik a vízbe helyezett hurkapálca sűrűsége az idő függvényében!

Közli: Varga István, Békéscsaba

Az elméleti versenyben kitűzött gyakorlatok és feladatok Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3732. a=10 cm külső élhosszúságú, d=2 cm falvastagságú, belül üres kocka térfogatának feléig elmerülve úszik a vizen.

Mekkora a fal anyagának sűrűsége?

(3 pont)

Közli: Holics László, Budapest

P. 3733. Ha kint hagyunk a kertben egy nyitott fémhordót, akkor néhány év múlva az alja ,,gömbölyű'' lesz. Miért?

(3 pont)

Közli: Simon Péter, Pécs

P. 3734. Függőleges síkban, R sugarú félkör alakú pályán súrlódás nélkül mozoghat egy kis golyó. Mekkora sebességgel kell az A pontból elindítani a golyót, hogy a B pontban a gyorsulása 3g legyen? Mozgása közben hol lesz a golyó gyorsulása vízszintes irányú? Mekkora itt a gyorsulás nagysága?

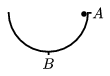
(5 pont)

Közli: Kobzos Ferenc, Dunaújváros

P. 3735. Ha a Földről naplementekor a Holdat félholdnak látjuk, milyennek látszik ugyanekkor a Holdról a Föld?

(4 pont)

Lánczos Kornél verseny, Székesfehérvár

P. 3736. Vízszintes felület felett h=0,95 m magasságban lévő R=0,2 m sugarú abroncsot \(\displaystyle \omega\)₀=5 s^-1 szögsebességgel megforgatunk, és kezdősebesség nélkül elengedünk. Az abroncs a vízszintes felülettel való ütközés után a felületet v=2 m/s sebességgel hagyja el, és \(\displaystyle \omega\)₁=3 s^-1 szögsebességgel forog.

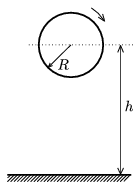
a) Mozgási energiájának hány százalékát veszítette el az abroncs az ütközés során?

b) Milyen szögben hagyja el az abroncs a vízszintes felületet?

(5 pont)

Közli: Kotek László, Pécs

P. 3737. Két azonos felépítésű ingaórát egyszerre elindítunk. A kettő közül csak az egyik pontos; ennek 777. lengésekor leng újra együtt a két inga. Hány százalékkal kell a pontatlan inga hosszát megváltoztatnunk, hogy pontos legyen?

(4 pont)

Közli: Bakonyi Gábor, Budapest

P. 3738. Egy háztetőn fekszik egy négyzet alakú rézlemez. Nem csúszik le, mert elég nagy a súrlódás. Nappal a hőmérséklet magasabb, éjjel alacsonyabb, ezért a fémlemez tágul és összehúzódik. Becsüljük meg, mennyit mozdul el a helyéről a lemez egy év alatt!

Adatok: A négyzet oldala 1 méter, a tető hajlásszöge 30^o, a súrlódási együttható 1, és a lemez egyenletesen nyomja a tetőt. A nappali és az éjjeli hőmérséklet különbsége átlagosan 10 ^oC, a tető hőtágulása elhanyagolható.

(5 pont)

Közli: Honyek Gyula, Budapest

P. 3739. 2 gramm héliumgázzal az ábrán látható körfolyamatot végeztetjük. A körfolyamat közben a gáz legalacsonyabb hőmérséklete 16 ^oC, a legmagasabb hőmérséklete 88 ^oC, közben az A és B állapotban a gáz hőmérséklete egyenlő.

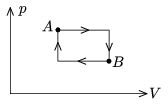
a) Hány ^oC-os a gáz az A és B állapotban?

b) Mennyi munkát végez a gáz a körfolyamatban?

c) Mennyi hőt vesz fel és mennyi hőt ad le a gáz egyetlen ciklus során?

(5 pont)

Közli: Radnai Gyula, Budapest

P. 3740. Egyenletes térfogati töltéssűrűségű, gömb alakú test elektrosztatikus potenciáljának értéke a gömb felületén hányad része a gömb középpontjában fellépő potenciálnak? (A potenciált a végtelenben választjuk nullának.)

(4 pont)

Példatári feladat

P. 3741. Egyenletes térfogati töltéssűrűségű, kocka alakú test elektrosztatikus potenciáljának értéke a kocka csúcsán hányad része a kocka középpontjában levő potenciálnak? (A potenciált a végtelenben választjuk nullának.)

(5 pont)

Amerikai versenyfeladat

P. 3742. Pontszerű hangforrásból gömbszimmetrikusan áramlik ki az energia, P teljesítménnyel. A hang terjedési sebessége v. Mekkora az energia térfogati sűrűsége és az energiaáram-sűrűség (egységnyi idő alatt egységnyi felületen átáramló energia) a hangforrástól r távolságban? Milyen az amplitúdó helyfüggése?

(4 pont)

Közli: Wiedemann László, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2004. november 11.