Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation
Already signed up?
New to KöMaL?

Exercises and problems in Physics
November 2004

Please read The Rules of the Problem Solving Competition.

Experimental problem

M. 255. Determine the moment of inertia of a cylindrical fruit-jar with respect to its generating (side) line. To improve the accuracy of the measurement, execute it as many ways as possible.

(6 points)

Theoretical problems

It is allowed to send solutions for any number of problems, but final scores of students of grades 9-12 are computed from the 5 best score in each month. Final scores of students of grades 1-8 are computed from the 3 best scores in each month.

P. 3743. At a given time, the distance recorder of a car showed 24 942 km. At exactly two hours later the driver noticed that it showed a symmetric number again. What was the average velocity of the car in this two-hour leg?

(3 points)

P. 3744. On a longer journey we drive 10% of the distance through inhabited areas at an average velocity of 40 km/h and 90% of the distance we drive on country roads at an average velocity of 90 km/h. What is the average velocity on the whole journey? How does this answer change if the percentages relate to time rather than distance, that is in 10% of the whole duration we drive in inhabited areas at an average speed of 40 km/h and 90% of the time we drive at an average speed of 90 km/h on country roads? In which case do we get there sooner?

(4 points)

P. 3745. Can a cyclist riding at a velocity of 36 km/h turn in a hairpin bend of a radius of 21 m (\(\displaystyle \mu\)=0.5)?

(4 points)

P. 3746. Above a heater in upward streaming air there are water droplets floating at a velocity of 1 mm/s. If two droplets join, at what constant velocity are they going to descend afterwards?

(5 points)

P. 3747. There are two solid balls of different radii but of the same composition. The mass of the bigger one is M. The balls are linked together with a long thin thread and let fall from a height. After they fall with constant velocity, what is the force pulling the thread? At what mass ratio is the pulling force greatest?

(5 points)

P. 3748. A flexible homogeneous rope is placed on a slope as shown in the figure. Determine the acceleration of the rope at the moment of release. (The friction is negligible.)

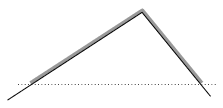
(4 points)

P. 3749. We can see special processes of a diatomic ideal gas in Figures a) and b). Determine the molar heat capacity of the gas in both processes.

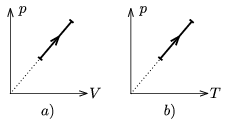
(4 points)

P. 3750. To a charged capacitor of electric capacity C we connect a discharged capacitor of capacity nC (n\(\displaystyle \ge\)1) in a parallel configuration. Then we disconnect and reconnect them with reversed polarity. Compare the voltage and electrostatic energy of the system in its final state to the initial voltage and electrostatic energy of capacitor C. What proportion is the decrease of voltage and energy?

(4 points)

P. 3751. What is the ratio of the magnitude of the magnetic induction vector in the middle of a circular current and at a point at distance r from it in the plane of the current if r\(\displaystyle \gg\)R?

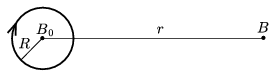
(5 points)

P. 3752. What is the closest distance an alpha-particle of energy of 5.3 MeV can get to the nucleus of a copper atom?

(4 points)

Send your solutions to the following address:

    KöMaL Szerkesztőség (KöMaL feladatok),
    Budapest 112, Pf. 32. 1518, Hungary
or by e-mail to:

Deadline: 11 December 2004