New exercises and problems in Mathematics
November 2004

Please read The Rules of the Problem Solving Competition.

New exercises for beginners Solutions can be submitted only by students of grade 9. Maximum score for each exercise (sign "K") is 6 points.

K. 13. Determine the last two digits of the sum 7¹+7²+...+7²⁰⁰⁵.

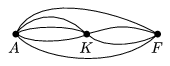
K. 14. There are several roads connecting three towns Downton, Upton and Middleton. The number of direct roads between any pair of towns is at least 3 and at most 10. There are 33 different paths from Downton to Upton, including roads that lead there directly as well as paths passing through Middleton. Similarly, one can go from Middleton to Upton directly or through Downton in 23 different ways. Given the information above, how many different paths are there altogether from Middleton to Downton (including direct roads as well as paths passing through Upton)? Example: In the Figure there are 2 direct roads from Downton (A) to Uptown (F) and there are 3^.2=6 paths through Middleton (K), which make 8 paths altogether.

K. 15. The convex quadrilateral ABCD has an angle of 100^o at vertex A. Given that the diagonal AC divides the quadrilateral into an equilateral triangle and an isosceles triangle, calculate the measures of the interior angles of the quadrilateral.

K. 16. a) Using each of the digits 9, 8, 7, 6 once, form two two-digit numbers such that their product is maximal. b) Using each of the digits 9, 8, 7, 6, 5, 4 once, form three two-digit numbers such that their product is maximal. Give reasons for your answer.

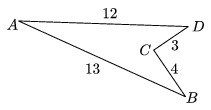
K. 17. The sides of the concave quadrilateral ABCD are AB=13 cm, BC=4 cm, CD=3 cm, DA=12 cm, and its interior angle at vertex C is 270^o. Find the area of the quadrilateral.

K. 18. Determine the four distinct digits a, b, c and d, such that \(\displaystyle \overline{abcd}:\overline{dcba}=4\), where \(\displaystyle \overline{abcd}\) and \(\displaystyle \overline{dcba}\) denote four-digit numbers.

K. 12. For how many positive numbers n is it true that 2004ⁿ is a factor of 2004! ? [2004! denotes the product of integers from 1 to 1024.] (Suggested by Á. Englert, Zalaegerszeg.)

New exercises Maximum score for each exercise (sign "C") is 5 points.

C. 780. There were three problems posed in a mathematics competition. The first problem was solved by 85 percent of the participants, the second one was solved by 80 percent and the last one by 75 percent. Prove that at least 40 percent solved all three problems.

C. 781. Find the positive primes p>q>r, such that p²- (q+r)²=136.

C. 782. A sailboat is travelling parallel to the shore of the lake Balaton, at a distance of 200 metres. A swimmer wants to reach the approaching sailboat by moving along a straight line. At what angle to the shore should he leave if the speed of the boat is 15 km/h, the speed of the swimmer is 2 km/h, and at start his distance from the point of the shore that is closest to the boat is 2 km? (Suggested by L. Koncz, Budapest)

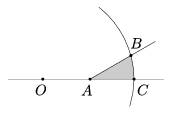
C. 783. The shaded region in the figure is bounded by the arms of the 30^o angle of vertex A and a circular arc centred at the point O. Find the area of the region, given that AO=AB=1.

C. 784. In the cuboid ABCDEFGH (with vertices labelled in the conventional way), AE= 1, AD = 2, AB =3. Find the volume of the solid whose vertices are A, C, and the midpoints of the edges around the face EFGH.

New problems The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3762. Two cylindrical tanks were filled with water. At 12 noon, two pumps of the same power started to pump the water, one from each tank, at a constant rate. At 2 p.m. the water levels were the same. At 5 p.m. the first tank was finished, and at 8 p.m. the second tank became empty, too. If the height of the second tank is 10 metres, how tall is the first one? (3 points)

B. 3763. P is a point in the interior of a convex quadrilateral ABCD. Prove that

PA²+PB²+PC²+PD²\(\displaystyle \ge\)2t_ABCD.

(3 points)

B. 3764. C₁ divides the side AB of an equilateral triangle ABC in a ratio 1:3. (It lies closer to A.) The points A₁, A₂ and A₃ divide the side BC into four equal parts. Find the sum of the angles AA₁C₁, AA₂C₁ and AA₃C₁. (4 points)

B. 3765. Given that the product of each pair out of 25 different positive integer not greater than 1000 is a perfect square, prove that the numbers themselves are also square numbers. (4 points)

B. 3766. There were four problems in a mathematics competition. The first problem was solved by 85 percent of the participants, the second one was solved by 80 percent, the third one was solved by 75 percent and the last one by 70 percent. What percentage of the participants, at least, must have solved all four problems? (4 points)

B. 3767. \(\displaystyle \alpha\), \(\displaystyle \beta\), \(\displaystyle \gamma\) are the angles of a triangle. Given that sin \(\displaystyle \alpha\)+sin \(\displaystyle \beta\)=(cos \(\displaystyle \alpha\)+cos \(\displaystyle \beta\))sin \(\displaystyle \gamma\), determine the angle \(\displaystyle \gamma\). (3 points)

B. 3768. A rectangle T₀ is cut into two non-congruent but similar rectangles T₁ and T₁' with a line parallel to a side. The procedure is repeated for the resulting rectangle T₁. Then it is repeated again for one of the parts obtained, and so on. Is there a rectangle T₀, such that the procedure can be repeated to infinity? (5 points)

B. 3769. Given three tangents and one focus of an ellipse, construct by ruler and compass, the other focus. (4 points)

B. 3770. Into how many parts do the planes of the faces of a regular octahedron divide the space? (5 points)

B. 3771. Let \(\displaystyle a_k=\frac{1}{\binom{n}{k}}\), \(\displaystyle b_k=\frac{1}{2^{n-k}}\), k = 1,2,...,n. Prove that

\(\displaystyle a_1+\frac{a_2}{2}+\frac{a_3}{3}+\dots+\frac{a_n}{n}=b_1+\frac{b_2}{2}+ \frac{b_3}{3}+\dots+\frac{b_n}{n}. \)

(5 points)

New advanced problems Maximum score for each advanced problem (sign "A") is 5 points.

A. 356. The sequence P_n(x) of polynomials is defined by the following recurrence: P₀(x)=0, P₁(x)=1 and P_n(x)=x^.P_n-1(x)+(1-x)^.P_n-2(x). What are the roots of P_n(x)?

A. 357. k₁,k₂,k₃, ... are disjoint circles. The radius of the circle k_i is \(\displaystyle \frac{1}{i}\) and its centre is P_i. Is it possible for the sequence of points P_i to be convergent?

A. 358. a, b, c are positive numbers, such that abc=1. Prove that

\(\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}-\frac{3}{a+b+c}\geq2\left( \frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\cdot\frac{1}{a^2+b^2+c^2}. \)

Send your solutions to the following address:

KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary

solutions@komal.hu.

Deadline:

10 December 2004 for problems K and

15 December 2004 for problems A, B, C.