A 2005. januári B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3782. Az $\displaystyle A=\overline{xyzu}$ és a $\displaystyle B=\overline{uzyx}$ tízes számrendszerben felírt négyjegyű számok szorzatának utolsó három számjegye 0. Keressük meg az összes ilyen tulajdonságú A, B számpárt.

(3 pont)

Megoldás: A két szám közül valamelyik osztható 5-tel, tegyük fel tehát először, hogy 5 | A. Ekkor A 0-ra vagy 5-re végződik. Mivel u=0 nem lehetséges, u=5, vagyis A páratlan. Az AB szám osztható 1000-rel, tehát B osztható 8-cal, így egyben páros szám is. Mivel x=0 sem lehetséges, B 5-tel nem osztható, vagyis A osztható kell legyen 125-tel. Innen az $\displaystyle \overline{yzu}$ szám lehetséges értékei 125, 375, 625 és 875. B utolsó számjegye a 8-cal való oszthatóság alapján innen már egyértelműen meghatározható: az első két esetben x=6, a másik két esetben pedig x=4. Az így nyert 4 lehetséges (A,B) számpár tehát (6125, 5216), (6375, 5736), (4625, 5264) és (4875, 5784). A feladat szimmetriája miatt az 5 | B esetben ugyanezt a négy számpárt kapjuk, csak minden egyes számpárban a két szám sorrendjét meg kell cserélnünk.

B.3783. Az ABCDE konvex ötszögben ABC$\displaystyle \angle$= CDE$\displaystyle \angle$= 90^o, BC=CD=AE=1, AB + ED = 1. Mekkora az ötszög területe?

(3 pont)

Megoldás: Forgassuk el a CDE háromszöget a C pont körül oly módon, hogy a D csúcs a B pontba kerüljön. Az így kapott CBE' háromszög az ABC háromszöggel együtt éppen az ACE' háromszöget adja ki, amely egybevágó az ACE háromszöggel, hiszen az AC oldal közös mindkettőben, CE=CE' és AE=1=AB+ED=AB+BE'=AE'. Az ötszög területe tehát éppen kétszerese az ACE' háromszög területének. Mivel ebben a háromszögben az egység hosszúságú AE' oldalhoz tartozó CB magasság is egységnyi hosszú, a háromszög területe 1/2, az ötszögé pedig éppen 1 területegység.

B.3784. Igazoljuk, hogy ha a, b, c pozitív számok, akkor

$\displaystyle 6a+4b+5c\ge5\sqrt{ab}+7\sqrt{ac}+3\sqrt{bc}. $

(3 pont)

Megoldás: A számtani és mértani közepek között fennálló egyenlőtlenség értelmében

$\displaystyle {a+b\over2}\ge\sqrt{ab},\quad{a+c\over2}\ge2\sqrt{ac},\quad{b+c\over2}\ge\sqrt{bc}.$

Az első egyenlőtlenséget 5-tel, a másodikat 7-tel, a harmadikat pedig 3-mal szorozva, a kapott három egyenlőtlenség összeadásával adódik a bizonyítandó állítás. Egyenlőség pontosan akkor áll fenn, ha az mindhárom helyen teljesül, vagyis a=b=c esetén.

B.3785. Egy számot szerencsésnek nevezünk, ha előáll olyan pozitív egészek összegeként, amelyek reciprokösszege 1. A 11 = 2 + 3 + 6 és a 4 = 2 + 2 például szerencsés számok, hiszen

$\displaystyle \frac{1}{2}+\frac{1}{3}+\frac{1}{6}=\frac{1}{2}+\frac{1}{2}=1. $

Szerencsés szám-e a 2005?

(4 pont)

Megoldás: A négyzetszámok nyilván mind szerencsés számok: az n² szám n pozitív egész összege, ahol minden összeadandó n-nel egyenlő, az összeadandók reciprokösszege pedig $\displaystyle n\cdot{1\over n}=1$. Ha pedig egy A szám k darab szerencsés szám összege, akkor kA is szerencsés szám lesz. Valóban, ha A=a₁+...+a_k, ahol az a_i szám `szerencsés' felírása $\displaystyle a_i=\sum_{j=1}^{r_i}b_{ij}$, akkor

$\displaystyle kA=\sum_{i=1}^k\sum_{j=1}^{r_i}kb_{ij},$

ahol az összeadandók reciprokösszege

$\displaystyle \sum_{i=1}^k\sum_{j=1}^{r_i}{1\over kb_{ij}}= {1\over k}\sum_{i=1}^k\sum_{j=1}^{r_i}{1\over b_{ij}}= {1\over k}\sum_{i=1}^k1=1.$

Mivel pedig 2005=5^.401, elegendő annyit megmutatni, hogy a 401 felírható 5 négyzetszám összegeként, ebből már következik, hogy a 2005 szerencsés szám. Ez pedig könnyen megtehető:

401=361+16+16+4+4=19²+4²+4²+2²+2².

B.3786. Adott 200 darab különböző valós szám. A számokat két csoportra osztjuk és mindkét csoportban nagyság szerint növekvően rendezzük az elemeket. Így kapjuk az a₁<a₂<...<a₁₀₀ és a b₁<b₂<...<b₁₀₀ sorozatokat. Ugyanezekből a számokból két újabb rendezett százas csoportot készítve az a₁'<a₂'< ...<a₁₀₀' és a b₁'<b₂'<...<b₁₀₀' sorozatokat kapjuk.

Bizonyítsuk be, hogy

|a₁-a₁'|+|a₂-a₂'|+...+|a₁₀₀-a₁₀₀'|=|b₁-b₁'|+|b₂-b₂'|+...+|b₁₀₀-b₁₀₀'|.

(5 pont)

Megoldás: Legyenek a számok nagyság szerint sorbarendezve s₁<s₂<...<s₂₀₀, és legyen 1$\displaystyle \le$i$\displaystyle \le$199 esetén d_i=s_i+1-s_i. Mind a baloldal, mind a jobboldal valamennyi összeadandója valamilyen d_j+d_j+1+...+d_j' alakú összeg, ahol 1$\displaystyle \le$j$\displaystyle \le$j'$\displaystyle \le$199. Elegendő azt megmutatni, hogy minden egyes 1$\displaystyle \le$i$\displaystyle \le$199 esetén d_i pontosan ugyanannyi |a_t-a'_t| alakú számban szerepel összeadandóként az egyenlőség baloldalán, mint ahány |b_t-b'_t| alakú tagban a jobboldon.

Tegyük fel, hogy az a₁,...,a₁₀₀ számok közül a_k a legnagyobb, amelyik még nem nagyobb s_i-nél, az a'₁,...,a'₁₀₀ számok közül pedig rendelkezzék éppen $\displaystyle a'_\ell$ ezzel a tulajdonsággal. Ekkor a b₁,...,b₁₀₀ számok között pontosan i-k olyan lesz, amely nem nagyobb s_i-nél, a b'₁,..., b'₁₀₀ számok között pedig az ilyenek száma pontosan i-$\displaystyle \ell$. Az általánosság megszorítás nélkül feltehetjük, hogy k$\displaystyle \ge$ $\ell$ . Ekkor az |a_t-a'_t| számban d_i pontosan akkor szerepel összeadandóként, ha $\ell$ < t $\le$ k, vagyis pontosan k- $\ell$ ilyen alakú számnak lesz d_i összeadandója. Hasonlóképpen, a |b_t-b'_t| számban akkor szerepel d_i összeadandóként, ha i-k< t $\le$ i- $\ell$ , vagyis szintén (i- $\ell$ )-(i-k)=k- $\ell$ alkalommal. Ezzel az állítást beláttuk.

B.3787. Az ABC háromszög belső pontja K, az AK, BK, CK egyenesek az A₁, B₁, C₁ pontokban metszik a szemközti oldalakat. Bizonyítsuk be, hogy

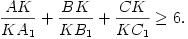
$\frac{AK}{KA_1}+\frac{BK}{KB_1}+\frac{CK}{KC_1}\ge6.$

(4 pont)

Megoldás: Legyenek $\alpha$ , $\beta$ , $\gamma$ olyan pozitív számok, melyekre CB₁:B₁A= $\alpha$ : $\gamma$ és BA₁:A₁C= $\gamma$ : $\beta$ , ekkor Ceva tétele miatt AC₁:C₁B= $\beta$ : $\alpha$ . Jelölje a 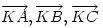$\overrightarrow{KA}, \overrightarrow{KB},\overrightarrow{KC}$ vektorokat rendre a,b,c. Ekkor

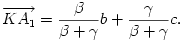
$\overrightarrow{KA_1}={\beta\over\beta+\gamma}b+{\gamma\over\beta+\gamma}c.$

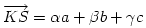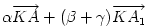A $\beta$ b+ $\gamma$ c vektor tehát párhuzamos az a vektorral. Ha tehát S az a pont, amelyre $\overrightarrow{KS}=\alpha a+\beta b+\gamma c$ , akkor az S pont az AA₁ egyenesre esik. Ugyanilyen alapon az S pont rajta van a BB₁ egyenesen is, vagyis S=K és $\alpha$ a+ $\beta$ b+ $\gamma$ c=0. Ezt $\alpha\overrightarrow{KA}+(\beta+\gamma)\overrightarrow{KA_1}$ alakba átírva látható, hogy AK:KA₁=( $\beta$ + $\gamma$ ): $\alpha$ . Ugyanígy kapjuk, hogy BK:KB₁=( $\alpha$ + $\gamma$ ): $\beta$ és CK:KC₁=( $\alpha$ + $\beta$ ): $\gamma$ . A bizonyítandó egyenlőtlenség tehát ekvivalens a

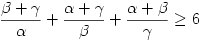
${\beta+\gamma\over\alpha}+{\alpha+\gamma\over\beta} +{\alpha+\beta\over\gamma}\ge6$

egyenlőtlenséggel, ami pedig ekvivalens az

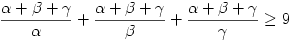
${\alpha+\beta+\gamma\over\alpha}+{\alpha+\beta+\gamma\over\beta} +{\alpha+\beta+\gamma\over\gamma}\ge9$

egyenlőtlenséggel. A baloldalon szereplő három tagot x,y,z-vel jelölve, a számtani és harmonikus közepek között fennálló egyenlőtlenség alapján

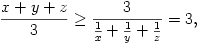
${x+y+z\over3}\ge{3\over{1\over x}+{1\over y}+{1\over z}}=3,$

vagyis x+y+z $\ge$ 9, és ezt kellett igazolnunk. Egyenlőség pontosan akkor áll fenn, ha x=y=z, vagyis ha $\alpha$ = $\beta$ = $\gamma$ , ami azt jelenti, hogy K az ABC háromszög súlypontja.

B.3788. Adott az ABC háromszög. Mi azon P pontok mértani helye a háromszög belsejében, amelyeknek az AB oldal egyenesétől mért távolsága számtani közepe a BC és a CA oldalak egyenesétől mért távolságának?

(4 pont)

Megoldás: A háromszög beírt körének középpontját jelölje K, az C csúcsból induló külső szögfelezőnek az AB egyenessel alkotott metszéspontja pedig legyen L. Jelölje továbbá M és N a KL egyenesnek az AC illetve BC oldallal alkotott metszéspontját. Állítjuk, hogy a keresett mértani hely az MN szakasz belső pontjainak halmaza, feltéve, hogy az L pont létezik, aminek szükséges és elégséges feltétele, hogy az AC és BC oldalak hossza különböző legyen. Az alábbi indoklás egyszerű módosításával az is könnyen látható, hogy az AC=BC esetben a keresett mértani hely a K ponton át az AB egyenessel párhuzamosan húzott egyenesnek a háromszög belsejébe eső szakasza lesz.

A P=K pontra nyilván teljesül a feltétel. Tegyük fel, hogy AC<BC, vagyis az A pont elválasztja az L és B pontokat. Az L pontnak az AC és BC egyenesektől mért távolsága megegyezik, az AB egyenestől mért távolsága pedig 0. Ha tehát nem csupán a háromszög belső pontjaira támaszkodunk és értelemszerűen előjeles távolságokkal számolunk, akkor a P=L pont is megfelelő lesz. Először is megmutatjuk, hogy ilyen értelemben a KL egyenes minden pontja megfelelő. Legyen D a KL egyenesnek az a pontja, amelynek K-tól L irányába mért előjeles távolsága éppen d. Ennek a pontnak az AB, AC, BC egyenesektől mért előjeles távolsága legyen c(d), b(d), illetve a(d), és tekintsük az 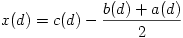$x(d)=c(d)-{b(d)+a(d)\over2}$ kifejezést. Mint láttuk, d=0 és d=KL esetén is x(d)=0. Ebből levezetjük, hogy minden d valós számra x(d)=0, ami éppen azt jelenti, hogy a KL egyenes minden pontja jó.

Jelölje az MLA, CMN és CNM szögek nagyságát rendre 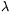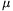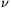$\lambda$ , $\mu$ , $\nu$ . Ekkor a(d)=a(0)+dsin 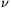$\nu$ , b(d)=b(0)-dsin 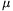$\mu$ és c(d)=c(0)-dsin 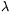$\lambda$ . Ezért

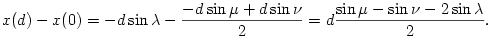
$x(d)-x(0)=-d\sin\lambda-{-d\sin\mu+d\sin\nu\over2}= d{\sin\mu-\sin\nu-2\sin\lambda\over2}.$

Mivel ennek a kifejezésnek az értéke d=KL $\ne$ 0 esetén 0, tetszőleges d érték esetén is 0 lesz, ami igazolja a fenti állítást.

Legyen most P tetszőleges pont, melynek az AB, AC, BC egyenesektől mért előjeles távolságát jelölje c(P), b(P), illetve a(P). Legyen D az a pont, amelyben a P-ből AB-re állított merőleges a KL egyenest metszi. Ha P a KL egyenesnek C-t tartalmazó oldalára esik, akkor c(P)>c(D), míg a(P)<a(D) és b(P)<b(D). Ezért ekkor 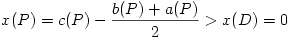$x(P)=c(P)-{b(P)+a(P)\over2}>x(D)=0$ . Hasonlóképpen, ha P a KL egyenesnek a másik oldalára esik, akkor x(P)<0. Vagyis x(P)=0 csak akkor teljesülhet, ha P a KL egyenesre esik. A keresett mértani hely tehát valóban a KL egyenesnek a háromszög belsejébe eső szakasza lesz.

B.3789. Hány olyan sík van, amely egy kockának legalább három élfelező pontján átmegy?

(4 pont)

Megoldás: A kockának van 4 testátlója. Egy testátlóra merőleges, a kocka középpontján áthaladó sík a kockát egy szabályos hatszögben metszi, melynek csúcsai élfelező pontok. Van tehát 4 olyan sík, amely pontosan hat éfelező ponton halad át.

A kocka lapjai pontosan 4 élfelező ponton haladnak át, ebből van 6 darab. A lapokkal párhuzamos szimmetriasíkok úgyszintén, ezekből 3 darab van. Tekinthetjük továbbá a kocka minden egyes éléhez az illető él végpontjaiból kiinduló négy további él felezőpontját, melyek egy téglalapot határoznak meg, ilyen módon találtunk 12 további síkot, mely pontosan négy élfelező pontra illeszkedik. Van tehát 6+3+12=21 olyan sík, amely pontosan négy élfelező ponton halad át.

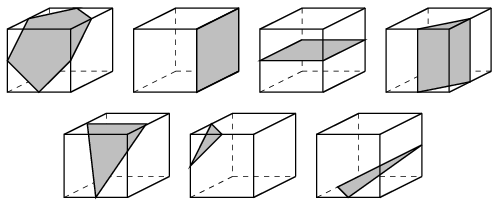
A kocka bármely élére illeszthetünk két olyan síkot, amely pontosan két további élfelező ponton halad át. Ez összesen 24 sík. További 8 síkot találunk, ha minden egyes csúcsra tekintjük az illető csúcsból induló élek felezőpontjaira illeszkedő síkot. Végül bármely két szomszédos élfelező pontra illeszkedik pontosan egy sík, amely pontosan egy további, egyikükkel sem szomszédos élfelező ponton halad át; ez 24 újabb síkot jelent. Van tehát 24+8+24=56 olyan sík, amely pontosan három élfelező ponton halad át.

Ez eddig összesen 4+21+56=81 megfelelő sík, a különböző lehetőségeket a mellékelt ábra mutatja. Most belátjuk, hogy ezzel már az összes lehetséges síkot megtaláltuk. Mivel 12 élfelező pont van, ezekből 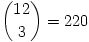${12\choose3}=220$ féleképpen választhatunk ki hármat. Számoljuk össze, hogy az áttekintett síkok ezek közül hány különböző hármast tartalmaznak. Az első 4 sík mindegyike 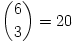${6\choose3}=20$ különböző hármast tartalmaz. A következő 21 sík mindegyike 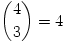${4\choose3}=4$ darabot, az utolsó 56 sík mindegyike pedig pontosan egyet. Az általunk talált síkok a 220 lehetséges hármasból összesen 4^.20+21^.4+56=220 darabot tartalmaznak, ami azt jelenti, hogy minden lehetséges hármasra illesztettünk már síkot. A keresett szám tehát a 81.

B.3790. Oldjuk meg a következő egyenletrendszert:

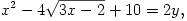
$x^2-4\sqrt{3x-2}+10=2y,$

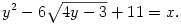
$y^2-6\sqrt{4y-3}+11=x.$

(5 pont)

Javasolta: Lorántfy László, Dabas

Megoldás: Az egyenletek baloldalát átalakítva az egyenletredszert így írhatjuk fel:

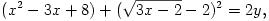
$(x^2-3x+8)+(\sqrt{3x-2}-2)^2=2y,$

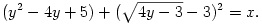
$(y^2-4y+5)+(\sqrt{4y-3}-3)^2=x.$

Innen látszik, hogy x²-3x+8 $\le$ 2y és y²-4y+5 $\le$ x. Mivel

x²-3x+8=(x-3/2)²+23/4,

kapjuk, hogy y $\ge$ 23/8>2. Továbbá

y²-4y+5=(y-2)²+1

miatt x $\ge$ (7/8)²+1>3/2 és 0<(y-2)²-1/2 $\le$ x-3/2 is fennáll. Ezért

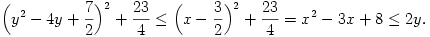
$\Bigl(y^2-4y+{7\over2}\Bigr)^2+{23\over4}\le\Bigl(x-{3\over2}\Bigr)^2+ {23\over4}=x^2-3x+8\le2y.$

A baloldali kifejezést kibontva az

y⁴-8y³+23y²-28y+18 $\le$ 2y

egyenlőtlenséget kapjuk, ami átrendezés és szorzattá alakítás után az

(y-3)²(y²-2y+2) $\le$ 0

alakra hozható. Minthogy az y²-2y+2 tényező értéke minden y valós számra pozitív, az egyenlőtlenség csak y=3 esetén állhat fenn. Ezt a második egyenletbe behelyettesítve x=2 adódik, és ez az x,y számpár valóban kielégíti az egyenletrendszert.

B.3791. A hegyesszögű ABC háromszög belsejében levő P pontra igaz, hogy APB $\angle$ =BPC $\angle$ = CPA $\angle$ . A BP és CP egyenesek az AC és AB oldalakat rendre D-ben és E-ben metszik. Mutassuk meg, hogy AB+AC $\ge$ 4DE.

(5 pont)

Olimpiai válogatóverseny feladata

Megoldás: Az APB, BPC, CPA, DPE szögek nagysága 120^o, az APE, BPE, APD, CPD szögeké pedig 60^o. Jelölje az A,B,C,D,E pontok P-től vett távolságát rendre a,b,c,d,e. A szögfelező-tétel és a koszinusz tétel alapján

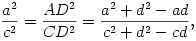
${a^2\over c^2}={AD^2\over CD^2}={a^2+d^2-ad\over c^2+d^2-cd},$

ahonnan beszorzás és rendezés után (c²-a²)d²=ac(c-a)d adódik. Ha a $\ne$ c, akkor ennek alapján d=ac/(a+c) adódik, ami nyilván az a=c esetben is teljesül. Hasonlóképpen, e=ab/(a+b).

Ismétcsak a koszinusz-tétel alapján AB²=a²+b²+ab, AC²=a²+c²+ac és DE²=d²+e²+de. Minthogy 4d $\le$ a+c és 4e $\le$ a+b (mindkét helyen egyenlőség egyszerre csak az a=b=c esetben állhat fenn), kapjuk, hogy

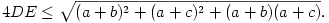
$4DE\le\sqrt{(a+b)^2+(a+c)^2+(a+b)(a+c)}.$

Ezért elegendő a

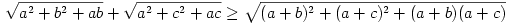
$\sqrt{a^2+b^2+ab}+\sqrt{a^2+c^2+ac}\ge\sqrt{(a+b)^2+(a+c)^2+(a+b)(a+c)}$

egyenlőtlenséget igazolni. Négyzetreemelés és rendezés után az egyenlőtlenség a

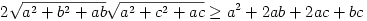
$2\sqrt{a^2+b^2+ab}\sqrt{a^2+c^2+ac}\ge a^2+2ab+2ac+bc$

alakot ölti, ami ismételt négyzetreemelés és rendezés után láthatóan ekvivalens a

3a⁴+3b²c²+4ab³+4ac³-4ab²c-4abc²-6a²bc $\ge$ 0

egyenlőtlenséggel. Lévén

3a⁴+3b²c²-6a²bc=3(a²-bc)² $\ge$ 0

és

4ab³+4ac³-4ab²c-4abc²=4a(b+c)(b-c)²,

az igazolni kívánt egyenlőtlenséget innen már leolvashatjuk.

A megoldásból az is világos, hogy egyenlőség csak az a=b=c esetben állhat fenn, vagyis ha az ABC háromszög szabályos (és akkor valóban fenn is áll).

Már regisztráltál?
Új vendég vagy?