Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation
Already signed up?
New to KöMaL?

Exercises and problems in Informatics
January 2005

Please read The Rules of the Problem Solving Competition.

New exercises of sign I

I. 94. Let us experiment with plane curves.

Write a program that has a real number a as its input, then displays the plane curve with equation (x2+y2)2=(x+ay)x2. Pay attention to the nice visualization. In demo mode, your program should give some examples of ``interesting'' values of the parameter a.

Your program (i94.pas) is to be submitted. (10 points)

I. 95. We are given a connected network of computers consisting of nodes and cables connecting two nodes. We want to make this network more secure such that it still remains connected if any of the cables (but only one of them!) breaks away. Determine those pairs of nodes - minimal in number - such that connecting them makes the network more secure in the above sense.

Every node is represented by a positive integer. Your program should read the pairs of numbers representing pairs of nodes. Each line of the input will consists of two positive integers separated by a space. The end of the input is indicated by two zeros, also separated by a space. Your program should display the pairs of nodes to be connected in the same format.

It is important that solutions will be checked by a computer program, so your program should not display anything else and should not make the output scrollable. (Hint: For testing purposes, your program can redirect stdin.)

Your program (i95.pas) is to be submitted. (10 points)

I. 96. The first n terms of a sequence do not specify the rest: in general, any number can stand at the (n+1)-th place.

We now give the following rule to determine the (n+1)-th term (supposing that n \(\displaystyle \ge\)2 is an integer and the first n terms of the sequence are already given):

The difference of consecutive terms are formed (that is the term with smaller index is subtracted from the one with larger index). Then we do the same operation on the difference sequence just obtained, and repeat the procedure again. After a few steps we arrive at a constant sequence with all terms equal: this will surely happen at most in the (n-1)-th step, since this time the sequence consists of only one term. For two examples, see the numbers in bold face in the table:

Your task is to find the (n+1)-th term of the original sequence such that forming difference sequences from the beginning will yield the same constant sequence. (See the thinner numbers at the rightmost columns in the example.)

Prepare a sheet (i96.xls) that constructs the (n+1)-th term of the sequence, if the first n terms are given, using the rule above.

Your sheet (i96.xls) is to be submitted. Remarks about its usage may be entered into cell A1. (10 points)

Our contestants are kindly asked to comply with the requirements given in the 2004 September issue of our Journal concerning the format (remarks, data, etc.) of your submitted works.

Send your solutions by e-mail to: i@komal.hu

New problem of sign S

S. 5. Write a program to draw Escher-like hypebolic tilings. Decompose Poincaré's disc model into triangles and draw the same pattern into each tile. The input consists of

  • Angles of the tile. The angles are \(\displaystyle \frac{180^\circ}{p}\), \(\displaystyle \frac{180^\circ}{q}\), \(\displaystyle \frac{180^\circ}{r}\), where p, q, r are positive integers such that \(\displaystyle \frac1p+ \frac1q+\frac1r<1\). Draw the starting triangle ABC such that A lies in the centre of the model and B is drawn right to (see the Figure, the subscriptions are ``Modell'' and ``Pattern'').

  • The common pattern of the tiles. The pattern is contained in a color, binary PPM file. The three vertices of the pattern triangle are specified by three coordinate pairs.

  • Resolution and file name for the output. The output is always square shaped so the resolution is a single positive integer m, at most 2048.

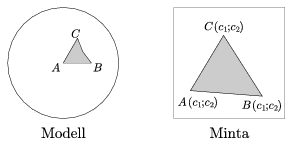
    The program gets the data as command-line parameters in the following:

    (program) p q r pattern.ppm a1 a2 b1 b2 c1 c2 output.ppm m

    (10 points)

    Send your solutions by e-mail to: s@komal.hu

    Deadline: 15 February 2005

    •