New exercises and problems in Mathematics
January 2005

Please read The Rules of the Problem Solving Competition.

New exercises for beginners Solutions can be submitted only by students of grade 9. Maximum score for each exercise (sign "K") is 6 points.

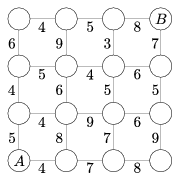
K. 25. The figure shows a rough map of a part of a city. The circles denote the crossroads, and the lines denote the roads connecting them. The number next to each road segment shows the number of minutes it takes to walk. What is the shortest possible time required to walk from point A to point B , given that one only proceeds upwards or to the right on the map?

K. 26. Alex and his father are talking: ``- Kid, how many pages is that book you have to read? - Less than 1000. - Have you started yet? - Yes. On Sunday, I read further than page 150. - And how much progress have you made today? - A lot! The sum of the numbers of the pages that I have read today is 2761.'' On what page did Alex start his reading on the day of this talk? How many pages had he read that day?

K. 27. Is there a square number of at least two digits, such that the digits are all different and in whatever order the digits are written down, the number will always be a perfect square? (Based on the idea of T. Halász)

K. 28. Determine all prime numbers p, such that 2p² +13 is also a prime.

K. 29. Prove that if we insert the same number of zeros between the digits of the number 121 in both places, (e.g. 10 201, 1 002 001 etc.), then we will always get the square of an integer.

K. 30. Prove that the sum of the diagonals of a convex quadrilateral is less than its perimeter but greater than half of the perimeter.

New exercises Maximum score for each exercise (sign "C") is 5 points.

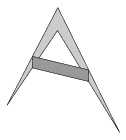
C. 790. The midpoints of the sides of a concave quadrilateral are connected as shown in the figure. Find the ratio of the area of the quadrilateral hence obtained to the area of the original quadrilateral.

C. 791. The fields of a 9 by 9 table are filled with the whole numbers from 460 to 540, starting in the top left corner and proceeding left to right row by row. We have an L-shaped board that covers four fields of the table. Is it possible to place it on the table so that the sum of the four numbers covered is 2005?

C. 792. Solve the following inequality: \(\displaystyle \sqrt{x^2+x}+x<\frac{1}{2}\).

C. 793. Find the exact value of

\(\displaystyle \sqrt[4010]{\frac{1}{2}\big(19+6\sqrt{10}\,\big)}\cdot\sqrt[2005]{3\sqrt{2}- 2\sqrt{5}} \)

C. 794. Two parallel planes intersect a sphere in two circles of areas 9\(\displaystyle \pi\) and 16\(\displaystyle \pi\), respectively. The planes are 1 unit apart. Find the surface area of the sphere.

New problems The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3782. \(\displaystyle A=\overline{xyzu}\) and \(\displaystyle B=\overline{uzyx}\) are four digit numbers in decimal notation. The last three digits of their product are zeros. Find all such pairs A, B of numbers. (3 points)

B. 3783. In the convex pentagon ABCDE, \(\displaystyle \angle\)ABC=\(\displaystyle \angle\)CDE=90^o, BC=CD=AE=1, AB +ED = 1. Find the area of the pentagon. (3 points)

B. 3784. Prove that if a, b, c are positive numbers, then

\(\displaystyle 6a+4b+5c\ge5\sqrt{ab}+7\sqrt{ac}+3\sqrt{bc}. \)

(3 points)

B. 3785. A number is called lucky number if it can be written as the sum of positive integers whose reciprocals add up to 1; 11 = 2 + 3 + 6 and 4 = 2 + 2, for example, are lucky numbers since

\(\displaystyle \frac{1}{2}+\frac{1}{3}+\frac{1}{6}=\frac{1}{2}+\frac{1}{2}=1. \)

Is 2005 a lucky number? (4 points)

B. 3786. A given set of 200 distinct real numbers are divided into two subsets of 100 elements each. The numbers in each subset are put in increasing order. The sequences a₁<a₂<...<a₁₀₀ and b₁<b₂< ...<b₁₀₀ are obtained. Then the whole procedure is repeated with the same numbers. The sequences obtained are a₁'<a₂'< ...<a₁₀₀' and b₁'<b₂'< ...<b₁₀₀'. Prove that

|a₁-a₁'|+ |a₂-a₂'|+ ...+ |a₁₀₀-a₁₀₀'|= |b₁-b₁'|+ |b₂-b₂'|+ ...+|b₁₀₀-b₁₀₀'|.

(5 points)

B. 3787. K is an interior point of the triangle ABC, and the lines AK, BK, CK intersect the opposite sides at the points A₁, B₁, C₁. Prove that

\(\displaystyle \frac{AK}{KA_1}+\frac{BK}{KB_1}+\frac{CK}{KC_1}\ge6. \)

(4 points)

B. 3788. Find the locus of those points P in the interior of a given triangle ABC, whose distance from the line of the side AB is the geometric mean of its distances from the line of the sides BC and CA. (4 points)

B. 3789. How many planes are there that pass through the midpoints of at least three edges of a cube? (4 points)

B. 3790. Solve the following simultaneous equations:

\(\displaystyle x^2-4\sqrt{3x-2}+10=2y,\)

\(\displaystyle y^2-6\sqrt{4y-3}+11=x.\)

(Suggested by L. Lorántfy, Dabas) (5 points)

B. 3791. P is a point in the interior of an acute-angled triangle ABC, such that \(\displaystyle \angle\)APB=\(\displaystyle \angle\)BPC=\(\displaystyle \angle\)CPA. The lines BP and CP intersect the sides AC and AB at D and E, respectively. Show that AB+AC\(\displaystyle \ge\)4DE. (5 points)

New advanced problems Maximum score for each advanced problem (sign "A") is 5 points.

A. 362. x₁, x₂,..., x_n are real numbers, such that

\(\displaystyle \sum_{i=1}^nx_i\ge n\) and \(\displaystyle \sum_{i=1}^nx_i^2\ge n^2\)

where n\(\displaystyle \ge\)3. Show that max  (x₁, x₂,..., x_n)\(\displaystyle \ge\)2.

A. 363. Is it possible to put together a cube 2005 units on edge out of cubes of edges 2, 3 and 7? (Suggested by A. Egri, Hajdúszoboszló)

A. 364. Prove that among any 19 given factors of 25! there are some whose product is a perfect cube.

Send your solutions to the following address:

KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary

solutions@komal.hu.

Deadline:

10 February 2005 for problems K and

15 February 2005 for problems A, B, C.