A 2005. februári B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3792. Az M pozitív egészből a tőle különböző N pozitív egész úgy származtatható, hogy M jegyeit valamilyen más sorrendben írjuk fel (első jegyük nem lehet nulla). Lehet-e mindkét szám a 2-nek pozitív egész kitevőjű hatványa?

(4 pont)

Megoldás: Tegyük fel, hogy N>M. Ha mindkét szám 2-hatvány, akkor N=2^aM, ahol a=2 vagy a=3, hiszen mindenképpen N<10M. Ekkor tehát N-M=3M vagy N-M=7M teljesül. Mivel N és M számjegyeinek összege megegyezik, 9-cel osztva ugyanolyan maradékot adnak, vagyis N-M osztható 9-cel. Ha azonban M 2-hatvány, akkor sem 3M sem 7M nem osztható 9-cel. A kérdésre tehát nemleges a válasz.

B.3793. Az ABCD négyzet belsejében adott a P pont. Tudjuk, hogy AP=1, BP=2, CP=3. Határozzuk meg a DP távolságot.

(3 pont)

Megoldás: Legyen a négyzet oldala a, a P pont BA és BC szakaszra eső vetületének B-től vett távolsága pedig rendre u és v. Pithagorasz tétele alapján u²+v²=BP²=4, és hasonlóképpen (a-u)²+v²=1 és u²+(a-v)²=9 is felírható. A két utóbbi egyenlőséget összeadva kapjuk, hogy

2a²+2(u²+v²)-2a(u+v)=10,

ahonnan

DP²=(a-u)²+(a-v)²=2a²+(u²+v²)-2a(u+v)=10-(u²+v²)=6,

vagyis \(\displaystyle DP=\sqrt{6}\).

B.3794. Bizonyítsuk be, hogy ha 0<q<p<1, akkor

p+3q<1+4pq.

(3 pont)

Megoldás: A bizonyítandó egyenlőtlenséget

\(\displaystyle -{1\over4}<\Bigl(2p-{3\over2}\Bigr)\Bigl(2q-{1\over2}\Bigr)\)

alakra hozva, nyilván csak azokat az eseteket kell megvizsgálni, amikor a jobboldalon szereplő két tényező közül az egyik negatív, a másik pedig pozitív.

Ha az első tényező pozitív, az azt jelenti, hogy 3/4<p<1 és 0<q<1/4. Ekkor

\(\displaystyle 0<2p-{3\over2}<{1\over2}\qquad\hbox{\rm\'es}\qquad-{1\over2}<2q-{1\over2}<0,\)

a két tényező szorzata tehát valóban nagyobb, mint -1/4.

A másik lehetőség az, hogy 1/4<q<p<3/4. Ekkor az u=3/2-2p és v=2q-1/2 jelöléseket bevezetve, u>0, v>0 és u+v=1+2(q-p)<1, ahonnan a számtani és mértani közepek között fennálló egyenlőtlenség szerint

\(\displaystyle \Bigl({3\over2}-2p\Bigr)\Bigl(2q-{1\over2}\Bigr)=uv\le\Bigl({u+v\over2}\Bigr)^2<{1\over4},\)

miként azt bizonyítani kívántuk.

B.3795. Adott két pont, amelyek távolsága 1 egység. Csak körző segítségével szerkesszünk két olyan pontot, amelyek távolsága \(\displaystyle \sqrt{2}\) egység.

(5 pont)

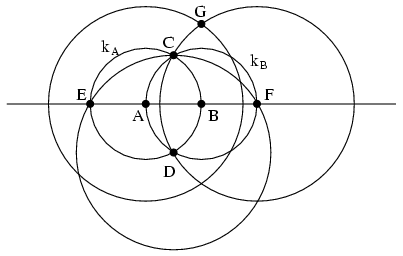
Megoldás: Legyen a két adott pont A és B. A, illetve B középponttal megrajzolva az egységsugarú k_A és k_B köröket, a létrejövő két metszéspontot jelölje C és D, ekkor \(\displaystyle CD=\sqrt{3}\). A Thalesz tétel és a Pithagorasz tétel alapján a D középpontú CD sugarú kör az AB egyenest olyan E és F pontokban metszi, amelyekre EA=AB=BF=1. A és F középpontokkal \(\displaystyle \sqrt3\) sugarú köröket rajzolva, jelölje G e két kör valamelyik metszéspontját. Ekkor az AFG egyenő szárú háromszögnek BG magassága a Pithagorasz tétel szerint éppen \(\displaystyle \sqrt2\) hosszúságú lesz.

B.3796. A k körhöz a külső A pontból érintőket húzunk, az érintési pontok E és F, az EF szakasz felezőpontja G. Egy A-n átmenő egyenes a B, C pontokban metszi a k kört. Bizonyítsuk be, hogy az EF egyenes felezi a BGC szöget.

(4 pont)

Megoldás: Ha a BC egyenes áthalad a G ponton, akkor az állítás nyilvánvaló, hiszen a BGE és a CGE szög is derékszög. Tegyük fel tehát, hogy nem ez a helyzet, és legyen B',C' a B,C pontok tükörképe az AG egyenesre, ekkor a BGC és B'GC' háromszögek egybevágók. Elegendő azt megmutatni, hogy a G pont illeszkedik a B'C szakaszra, hiszen ebből következik az, hogy a BGE és C'GF szögek váltószögek, a C'GF szög pedig szimmetria okok miatt egyenlő a CGE szöggel.

A bizonyításhoz vegyünk fel egy derékszögű koordinátarendszert oly módon, hogy a kör egyenlete x²+y²=1 legyen, a G pont koordinátái pedig G(0,a) legyenek, ahol 0<a<1. Feltehetjük, hogy a B és C pont x koordinátái negatív számok. A kör középpontja az O origó lesz, az OEG és OAE derékszögű háromszögek hasonlósága miatt pedig az A pont koordinátái A(0,1/a). A BC egyenes egyenlete ekkor y=mx+1/a alakú, a B'C' egyenesé pedig y=-mx+1/a, ahol m alkalmas pozitív szám, amit akár ki is fejezhetnénk a segítségével, de erre nem lesz szükség. Jelölje a B és C pontok koordinátáit B(x₁,y₁) illetve C(x₂,y₂), ahol feltehető, hogy x₂<x₁<0. A B' és C' pontok koordinátái tehát B'(-x₁,y₁), illetve C'(-x₂,y₂). A B',G,C pontok kollinearitása ezek szerint így fogalmazható meg:

\(\displaystyle {-x_1\over y_1-a}={x_2\over y_2-a}.\)

Lévén y_i=mx_i+1/a, a következő egyenlőséget kell belátnunk:

\(\displaystyle -x_1\Bigl(mx_2+{1\over a}-a\Bigr)=x_2\Bigl(mx_1+{1\over a}-a\Bigr),\)

vagy, ami ezzel ekvivalens:

\(\displaystyle 2mx_1x_2+{1-a^2\over a}(x_1+x_2)=0.\)

Minthogy x₁,x₂ az y=mx+1/a egyenletű egyenes és az x²+y²=1 egyenletű kör két metszéspontjának x koordinátái, kielégítik az x²+(mx+1/a)²=1 egyenletet, vagyis az

\(\displaystyle (m^2+1)x^2+{2m\over a}x+{1-a^2\over a^2}\)

másodfokú egyenlet megoldásaiként kaphatók meg. A gyökök és együtthatók közötti összefüggés szerint tehát

\(\displaystyle x_1x_2={1\over m^2+1}\cdot{1-a^2\over a^2},\qquad x_1+x_2=-{1\over m^2+1}\cdot{2m\over a}.\)

A bizonyítandó állítás ezek szerint a

\(\displaystyle {2m\over m^2+1}\cdot{1-a^2\over a^2} -{1-a^2\over a}\cdot{1\over m^2+1}\cdot{2m\over a}=0\)

alakba írható, ami pedig nyilvánvalóan teljesül.

B.3797. Adott az ABC szabályos háromszög. Mi azon P pontok mértani helye a háromszög belsejében, amelyeknek az AB oldaltól mért távolsága mértani közepe a BC és a CA oldaltól mért távolságának?

(4 pont)

Megoldás: Vegyünk fel egy derékszögű koordinátarendszert, amelyben az A,B,C pontok koordinátái rendre A(-1,0), B(1,0) és \(\displaystyle C(0,\sqrt{3})\). A háromszög S középpontjának koordinátái \(\displaystyle S(0,1/\sqrt{3})\), ezt az AB szakaszra tükrözve kapjuk a \(\displaystyle T(0,-1/\sqrt{3})\) pontot. A Pithagorasz-tétellel könnyen ellenőrizhető, hogy \(\displaystyle AT=BT=ST=2/\sqrt{3}\). Ugyan az A,B pontok nem esnek a háromszög belsejébe, a feltétel nyilván teljesül rájuk, és az S pontra is. Megsejthetjük tehát, hogy a keresett mértani hely a T középpontú, S-re illeszkedő körvonalnak a háromszög belsejébe eső része, ami nem más, mint az ASB mindkét végén nyitott körív. Hogy ez az ív teljes egészében a háromszög belsejébe esik, onnan látszik, hogy TC²=AC²+TA²=16/3 miatt az AC egyenes érinti az említett kört, és ugyanez igaz a BC egyenesre is.

Ha a P(x,y) pont a körívre esik, akkor

\(\displaystyle x^2+\Bigl(y+{1\over\sqrt{3}}\Bigr)^2=\Bigl({2\over\sqrt{3}}\Bigr)^2,\)

vagyis \(\displaystyle y^2=1-x^2-(2/\sqrt{3})y\). A BC egyenes egyenlete \(\displaystyle x+y/\sqrt{3}=1\), vagyis a P pont távolsága az egyenestől \(\displaystyle (\sqrt{3}/2)|x+y/\sqrt{3}-1|\). Hasonlóképpen, a P pont AC egyenestől mért távolsága \(\displaystyle (\sqrt{3}/2)|-x+y/\sqrt{3}-1|\). A két távolság szorzata

\(\displaystyle {3\over4}\Bigl|\Bigl(1-{y\over\sqrt{3}}\Bigr)^2-x^2\Bigr|= \Bigl|{1\over4}y^2+{3\over4}\Bigl(1-x^2-{2\over\sqrt{3}}y\Bigr)\Bigr|=y^2,\)

ami mutatja, hogy a körvonal pontjai eleget tesznek a feltételnek (akkor is, ha nem esnek a háromszög belsejébe).

Már csak azt kell megmutatnunk, hogy ha a háromszög belsejében lévő P pont nem esik a körívre, akkor nem teljesíti a feltételt. Jelölje Q a P-ből az AB oldalra emelt merőlegesnek a körívvel alkotott metszéspontját, erre a pontra tehát teljesül a feltétel. Ha a P pont közelebb van az AB oldalhoz, mint a Q pont, akkor mind az AC, mind pedig a BC oldaltól mért távolsága nagyobb lesz, mint a Q ponté, vagyis az AB oldaltól vett távolság kisebb lesz, mint a másik két oldaltól vett távolság mértani közepe. Ellenkező esetben pedig nagyobb lesz, vagyis egyenlőség tényleg csak a körív pontjaira állhat fenn.

B.3798. Legyen \(\displaystyle \alpha=2+\sqrt{3}\). Bizonyítsuk be, hogy minden pozitív egész n-re

[\(\displaystyle \alpha\)ⁿ]=\(\displaystyle \alpha\)ⁿ+\(\displaystyle \alpha\)^-n-1.

(4 pont)

Megoldás: Mivel \(\displaystyle (2+\sqrt{3})(2-\sqrt{3})=1\), látható, hogy \(\displaystyle 0<1/\alpha=2-\sqrt{3}<1\), vagyis \(\displaystyle 0<\alpha^{-n}=(2-\sqrt{3})^n<1\). A binomiális tétel alapján tehát

\(\displaystyle N=\alpha^n+\alpha^{-n}=2\sum_{i=0}^{[n/2]} {n\choose2i}2^{n-2i}\sqrt{3}^{2i}\)

egész szám, melyre \(\displaystyle \alpha\)ⁿ<N<\(\displaystyle \alpha\)ⁿ+1. Ezért [\(\displaystyle \alpha\)ⁿ]<N\(\displaystyle \le\)[\(\displaystyle \alpha\)ⁿ]+1, vagyis

[\(\displaystyle \alpha\)ⁿ]+1=N=\(\displaystyle \alpha\)ⁿ+\(\displaystyle \alpha\)^-n,

ahonnan a bizonyítandó állítás leolvasható.

B.3799. Két egybevágó szabályos háromszög közös része egy hatszög. Bizonyítsuk be, hogy ebben a hatszögben a másodszomszédos oldalak hosszának összege egyenlő.

(4 pont)

Megoldás: A hatszöghöz illeszkedő hat kis háromszög egyikének az oldalai legyenek x,y,z. Mivel ezek a háromszögek hasonlók, alkalmas a,b,c,d,e pozitív számokkal oldalaik hossza az ábrán látható módon írható fel.

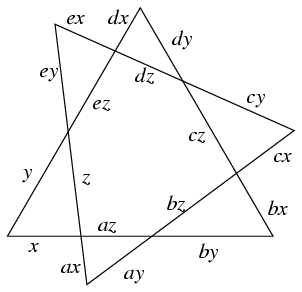
Ekkor a bizonyítandó állítás így fogalmazható meg: z+bz+dz=az+cz+ez, vagyis az A=1+b+d, B=a+c+e jelölésekkel élve, A=B. Az egyik szabályos háromszög oldalainak összege

(x+az+by)+(bx+cz+dy)+(dx+ez+y)=Ax+Ay+Bz,

míg a másik háromszög oldalainak összege

(ay+bz+cx)+(cy+dz+ex)+(ey+z+ax)=Bx+By+Az.

Mivel a két szabályos háromszög egybevágó, ez a két összeg egyenlő, vagyis A(x+y-z)=B(x+y-z). A háromszög-egyenlőtlenség miatt azonban x+y-z>0, vagyis valóban A=B.

B.3800. Egy kocka minden csúcsában ül egy-egy hangya. Egy adott pillanatban mindegyikük elindul egy véletlenszerűen kiválasztott élen, és átmászik rajta a szomszédos csúcsba. Mennyi annak a valószínűsége, hogy két hangya találkozik útközben vagy az út végén?

(4 pont)

Megoldás: Hogyan lehetséges az, hogy semelyik két hangya nem találkozik? Ha egy hangya elindul az A₁ csúcsból az A₁A₂ élen, akkor az A₂ csúcsban lévő hangyának egy A₂A₃ élen kell elindulni, ahol A₁\(\displaystyle \ne\)A₃. Az A₃ csúcsban lévő hangyának egy A₃A₄ élen kell elindulni, és így tovább, majd előbb vagy utóbb a kör bezárul, és egy olyan A₁,A₂,..., A_n,A_n+1 csúcssorozathoz jutunk, ahol i=1,2,...,n esetén az A_i csúcsban lévő hangya az A_iA_i+1 élen indul el, A₁,A₂,...,A_n különböző csúcsok, és A_n+1 az A₁,A₂,...,A_n-1 csúcsok valamelyike. Ez a csúcs csakis A₁ lehet, mert ha A_i volna valamilyen 2\(\displaystyle \le\)i\(\displaystyle \le\)n-1 esetén, akkor az n-edik hangya és az i-1-edik hangya ugyanabba a csúcsba érkezne. A hangyák útvonalai tehát a kocka élgráfjában néhány csúcsdiszjunkt kört alkotnak, melyek az összes csúcsot lefedik. A kocka élgráfjában csak páros hosszú körök vannak, hiszen 1-essel jelölt csúcsból csak 2-essel jelölt csúcsba vezet él, és fordítva, 2-essel jelölt csúcsból csak 1-essel jelölt csúcsba vezet él. Két lehetőség van tehát, vagy két diszjunkt 4 hosszúságú kört kapunk, vagy pedig egyetlen kört, ami mind a 8 csúcson áthalad. Az első eset csak úgy valósulhat meg, ha a két kör két egymással párhuzamos lapon megy körbe, a második eset pedig csak úgy, ha valamelyik lapon megteszünk egy 3 élből álló utat, átmegyünk az illető lappal párhuzamos lapra, ott is megteszünk egy 3 hosszúságú utat (fordított körüljárás szerint), majd visszatérünk a kiindulási csúcsba, ahogyan az az ábrán látható.

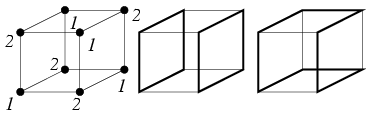
Mivel mind a 8 hangya három különböző élen indulhat el, összesen 3⁸ különböző eset képzelhető el, melyek mindegyike ugyanakkora valószínűséggel következik be. Hány olyan eset van ezek között, amelyikben semelyik két hangya nem találkozik egymással? Ha két diszjunkt kört kaptunk, akkor az egy párhuzamos lappárhoz tartozik, amit 3 különböző módon választhatunk ki. Mivel mindkét lapon a hangyák tetszőleges körüljárás szerint mehetnek körbe, ez összesen 3x4=12 eset. Ha egyetlen kört kaptunk, akkor ahhoz is hozzárendelhetünk egy párhuzamos lappárt, azt a két lapot, amelyekre a körnek csak két éle illeszkedik. Ha ezek közül az egyiken tekintjük a kör két élét, azok egymással párhuzamosak, és ez a két él a kört már egyértelműen meghatározza, 6 ilyen kör van tehát. Mivel a körön két különböző körüljárás szerint mehetnek a hangyák körbe, ez összesen 12 újabb esetet jelent. Ezek szerint összesen 24 rossz eset van, a keresett valószínűség tehát

\(\displaystyle 1-{24\over3^8}=1-{8\over3^7}\approx0,99634.\)

B.3801. Jelölje P(n) az első n pozitív prímszám összegét. Bizonyítsuk be, hogy P(n) és P(n+ 1) között van négyzetszám.

(5 pont)

Megoldás: Mivel P(1)=2, P(2)=5, P(3)=10, P(4)=17 és P(5)=28, látszik, hogy az állítás igaz, ha n\(\displaystyle \le\)4. Tegyük fel, hogy n\(\displaystyle \ge\)4, és az állítást n-re már igazoltuk. Legyen k a legnagyobb egész szám, amelyre teljesül, hogy P(n)<k²<P(n+1). Megmutatjuk, hogy (k+1)² és (k+2)² közül legalább az egyik P(n+1) és P(n+2) közé esik. Ebből a teljes indukció elve alapján következik a bizonyítandó állítás.

Jelölje p_n az n-edik prímszámot. Mivel p₅=11=2^.4+3, és n>1 esetén p_n+1\(\displaystyle \ge\)p_n+2, látható, hogy n\(\displaystyle \ge\)4 esetén p_n+1\(\displaystyle \ge\)2n+3 teljesül, amiből a számtani és mértani közepek között fennálló egyenlőtlenség segítségével könnyen levezethető, hogy

\(\displaystyle (n+1)(p_{n+1}-n)<\Bigl({p_{n+1}+1\over2}\Bigr)^2.\)

Ezért n\(\displaystyle \ge\)4 esetén k²<P(n+1) alapján

\(\displaystyle k^2\le P(n+1)-1\le1+3+5+\ldots+(p_{n+1}-2)+p_{n+1} =\Bigl({p_{n+1}+1\over2}\Bigr)^2,\)

ahonnan 2k-1\(\displaystyle \le\)p_n+1, vagyis 2k+1\(\displaystyle \le\)p_n+2. Ha tehát (k+1)²>P(n+1), akkor

P(n+1)<(k+1)²=k²+2k+1<P(n+1)+p_n+2=P(n+2).

Ha pedig k²=P(n+1), akkor így okoskodhatunk:

(k+1)²\(\displaystyle \le\)p_n+1+(p_n+1-2)+(p_n+1-4)+...+(p_n+1-2n)=

\(\displaystyle =(n+1)(P_{n+1}-n)<\Bigl({p_{n+1}+1\over2}\Bigr)^2,\)

ahonnan 2k+2<p_n+1+1, és ezáltal 2k+3< p_n+2 adódik. Ezért ebben az esetben

P(n+1)<(k+2)²=(k+1)²+2k+3<P(n+1)+p_n+2=P(n+2).