 Problem A. 379. (September 2005)
Problem A. 379. (September 2005)
A. 379. Find all real numbers 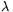 for which there exists a non-zero polynomial P, such that
for which there exists a non-zero polynomial P, such that
for all n. List all such polynomials for 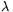 =2.
=2.
(5 pont)
Deadline expired on October 17, 2005.
Sketch of solution. Let P(x)=a0+a1x+...+akxk. Both sides of the equation contains a polynomial of n, degree is k. The coefficients must pairwise match.
Since the coefficient of nk is
on the left-hand side, and it is
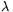 ak on the right-hand side. Therefore,
ak on the right-hand side. Therefore, .
If then we have a homogenous system of linear equations for the coefficients and one of these equations vanishes. So the system has infinitely many solutions.
For 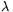 =2 we obtain k=3 and P(x)=c(x3-x).
=2 we obtain k=3 and P(x)=c(x3-x).
Statistics:
15 students sent a solution. 5 points: Erdélyi Márton, Estélyi István, Gyenizse Gergő, Kónya 495 Gábor, Nagy 224 Csaba, Paulin Roland, Tomon István. 4 points: Jankó Zsuzsanna, Molnár 999 András. 3 points: 2 students. 1 point: 1 student. 0 point: 3 students.
Problems in Mathematics of KöMaL, September 2005
