Problem A. 383. (November 2005)
Problem A. 383. (November 2005)
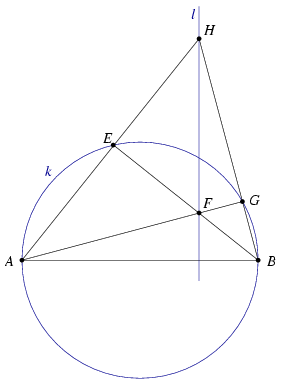
A. 383. The diameter AB of the circle k is perpendicular to the line  , which does not pass through either A or B. Let C be a point of
, which does not pass through either A or B. Let C be a point of  outside k, and let D denote the other intersection of the line AC with the circle. Draw one of the tangents from C to k and denote the point of contact by E. Let F be the intersection of the lines BE and
outside k, and let D denote the other intersection of the line AC with the circle. Draw one of the tangents from C to k and denote the point of contact by E. Let F be the intersection of the lines BE and  , and finally let G denote the intersection of the line segment AF with k. Show that the line DF passes through the reflection of the point G about AB.
, and finally let G denote the intersection of the line segment AF with k. Show that the line DF passes through the reflection of the point G about AB.
Based on a problem from Germany, suggested for the IMO
(5 pont)
Deadline expired on December 15, 2005.
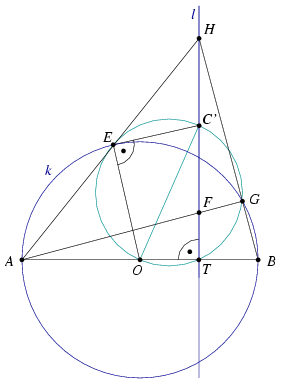
Solution 1. Denote the intersection of lines AE and BG by H. The orthocenter of triangle ABH is F and also H lies on l (Figure 1).
|
|
|
| Figure 1 | Figure 2 |
Let O and C' be the midpoints of AB and HF and denote by T the intersction of l and AB. The 9-point circle of triangle ABH passes through points E, G, O, T and C'. From the right angle at T we know that OC' is a diameter of the 9-point circle and CEO =90o. Therefore C'E is perpendicular to OE which is a radius of k. This implies that C'=C and CE=CF=CG=CH. Finally, CG touches k (Figure 2).
=90o. Therefore C'E is perpendicular to OE which is a radius of k. This implies that C'=C and CE=CF=CG=CH. Finally, CG touches k (Figure 2).
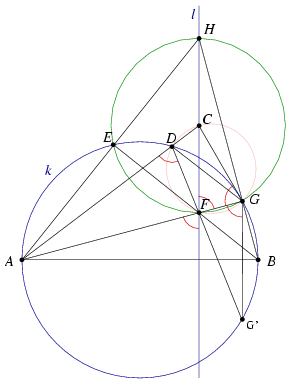
3. ábra
Now consider the inversion with pole A which maps k and l to each other. Points C,D and F,G are images of each other so these four point lie on a circle (Figure 3).
Denote by G' the second intersection of DF and k. Then
G'GA =G'DA
=G'DA =180o-CDF
=180o-CDF =FGC
=FGC =CFG
=CFG .
.
and GG' is paralel to l and perpendicular to AB.
Remark. Since several possible configurations of the figure exist, one must use signed angles or consider each cases separately.
Solution 2. Denote by H the intersection of lines BD and EG. Apply Pascal's thorem to the degenerate hexagon EEBDAG. You obtain that F, C and H lie on a line which is l (Figure 4).
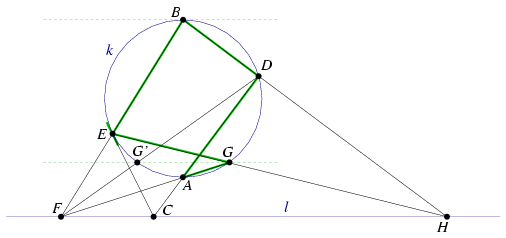
Figure 4
Let G' be the second intersection of k and l. Now apply Pascal's thorem for the degenerate hexagon GG'DBBE (Figure 5). You obtain that line GG' passes through the ideal intersection of l and the tangent line at B. Therefore, GG' is parallel to l and perpendicular to AB.
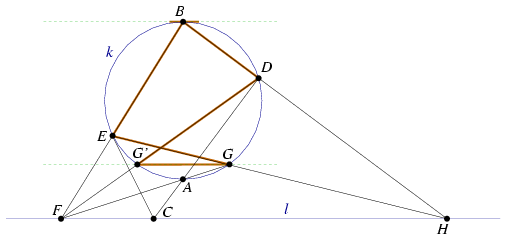
Figure 5
Statistics:
13 students sent a solution. 5 points: Bogár 560 Péter, Jankó Zsuzsanna, Nagy 224 Csaba, Paulin Roland. 4 points: Hujter Bálint, Kisfaludi-Bak Sándor, Tomon István. 3 points: 5 students. 0 point: 1 student.
Problems in Mathematics of KöMaL, November 2005