Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation
Already signed up?
New to KöMaL?

Problem A. 386. (December 2005)

A. 386. Consider one of the two arcs of a rectangular hyperbola centred at O, and choose an arbitrary point P on it. Let Q and R denote the intersections of the hyperbola and the circle of radius 2OP drawn about P. Prove that \angleQPR=120o.

(5 pont)

Deadline expired on January 16, 2006.

Solution. Place the hyperbola into the Cartesian co-ordinate system such that its equation is xy=1. Draw the other branch of the hyperbola as well. The circle and the second branch have another 2 intersections: S and P' which is the reflection of P to O.

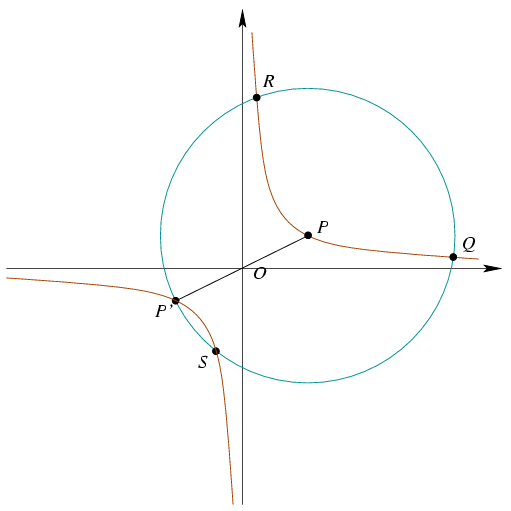
Let P=(a,b) and compute the intersections of the hyperbola and the circle. A point (x,y) lies on both curves if and only if

xy=1

and

(x-a)2+(y-b)2=4(a2+b2).

Then

(x-a)^2+\left(\frac1x-b\right)^2=4(a^2+b^2)

x4-2ax3-3(a2+b2)x2-2bx+1=0.(1)

Let P'=(-a,-b), Q=(q1,q2), R=(r1,r2) and S=(s1,s2). The roots of the quartic equation (1) are exactly -a, q1, r1 and s1.

From Viéte's formulas, the sum of roots is 2a. Therefore

q1+r1+s1=3a.(2)

Similarly,

q2+r2+s2=3b.(3)

Equations (2) and (3) together yield that P is the centroid of triangle QRS. But P is the circumcenter as well. This implies that triangle QRS is equilateral, point P is its center anf \angleQPR=120o.

Statistics:

14 students sent a solution.
5 points:Bogár 560 Péter, Erdélyi Márton, Estélyi István, Hujter Bálint, Jankó Zsuzsanna, Kisfaludi-Bak Sándor, Kónya 495 Gábor, Nagy 224 Csaba, Paulin Roland, Szakács Nóra, Tomon István.
4 points:Dücső Márton.
2 points:1 student.
0 point:1 student.

Problems in Mathematics of KöMaL, December 2005