 Problem A. 387. (December 2005)
Problem A. 387. (December 2005)
A. 387. We have n marbles that look all alike, but we know that one of them is radioactive. We want to find that marble. We also have a detector that can determine whether any chosen subset of the marbles contains the radioactive marble or not. We want to choose a measurement strategy for which the expected number of measurements is a minimum. Find that smallest expected value possible.
(5 pont)
Deadline expired on January 16, 2006.
Solution 1. Denote by an the expected value of measures for an optimal strategy. We show that if 2k n
n 2k+1 then
2k+1 then
Introduce also bn=nané the statement is
bn=kn+2(n-2k).
Apply induction. Trivially a1=0 and a2=1. Now let n 2 and assume that the statement is true for all smaller indices.
2 and assume that the statement is true for all smaller indices.
Let the number of the measured marbles in the first measuremebt be x. We have the probability is x/n that the radioactive one is among those x marbles and we expect another ax measurements. Therefore, the expected number of measurements will be
and
| (1) |
It is easy to check that for all m<n-1 we have bm+1-bm=[log2m]+2 which is increasing. Therefore, sequence b1,...,bn-1 is convex and we obtain the minimum in (1) when x=[n/2]. (The minimum is not necessarily unique.) Then x,n-x [2k-1,2k] and
[2k-1,2k] and
bn=n+bx+bn-x=n+((k-1)x+2(x-2k-1))+((k-1)(n-x)+2(n-x-2k-1))=kn+2(n-2k).
Solution 2. Encode the strategy by a binary graph. Each state of the procedure is represented by a vertex. Assing the lists of suspicious marbles to the vertices. If there are more than one suspicious marbles at a vertex then the vertex has two children. The leaves of the tree are those vertices where there are single marbles; they represent the possible ends of the strategy. Figure 1 shows the tree for the strategy when the marbles are measured one by one.
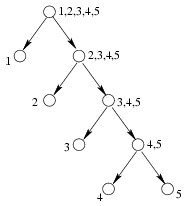
Figure 1
On the other hand, each binary tree with n leaves represent a strategy. To reproduce the strategy, first write the numbers 1,2,...,n to the leaves then write the union of the children to each vertex (Figure 2).

Figure 2
The expected number of measurements is the average depth of the leaves. Denote the minimum and maximum of those depths by a and b. If b>a+1 then the sum of depths can be decreased (Figure 3). So an optimal strategy uses at most two consecutive depths.
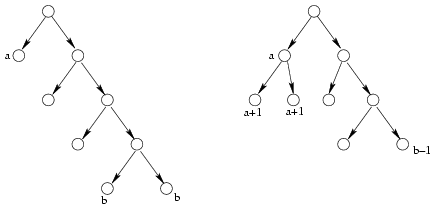
Figure 3
Let the two depths be k and k+1 and the number of leaves at depth (k+1) be x. Then n=2k+x and 2k n
n 2k+1. The average depth is
2k+1. The average depth is
Statistics:
14 students sent a solution. 5 points: Erdélyi Márton, Estélyi István, Gyenizse Gergő, Hujter Bálint, Jankó Zsuzsanna, Nagy 224 Csaba, Paulin Roland, Sümegi Károly, Tomon István. 4 points: Ureczky Bálint. 3 points: 3 students. 0 point: 1 student.
Problems in Mathematics of KöMaL, December 2005
