Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation
Already signed up?
New to KöMaL?

Problem A. 392. (February 2006)

A. 392. The inradius of a tetrahedron is r. There exists three spheres which touch the four face planes such that all touching points are outside the surface of the tetrahedron; the radii of those spheres are r1, r2 and r3. Show that r1+r2+r3>9r.

(5 pont)

Deadline expired on March 16, 2006.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Először is megjegyezzük, hogy bizonyos esetektől eltekintve mindig nyolc olyan gömb létezik, ami érinti a tetraéder összes lapsíkját. Másképpen, nyolc olyan pont létezik a térben, ami mind a 4 lapsíktól egyenlő távolságra van.

Legyenek a tetraéder csúcsai A,B,C,D. Egy pont akkor és csak akkor van egyenlő távolságra az ABC és ABD síkoktól, ha ezek valamelyik szögfelező síkján fekszik. A két szögfelező sík egymásra merőleges és illeszkedik az AB egyenesre. Hasonlóan, a gömb közéépontjának illeszkednie kell a tetraéder AC és BC élén fekvő valamelyik szögfelező síkra. Mindegyik élnél két sík közül választhatunk, ez 8 lehetőség. A 3 kiválasztott síknak mindegyik esetben legfeljebb 1 közös pontja van.

Természetesen előfordul, hogy a három sík három párhuzamos egyenesben metszi egymást, és ezért valamelyik pont nem jön létre.

A 8 gömb közül az egyik a tetraéder beírt gömbje. Mindig létezik 4, a lapokhoz írt gömb, ami a tetraéderen kívül fekszik, és az adott lapot egy belső pontban érinti. További 3 gömb a tetraéder szemközti élpárjaihoz tartozhat, az ábra szerint.

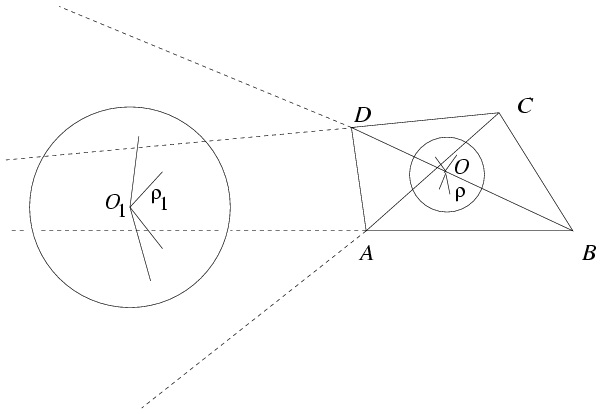
Jelöljük a lapok területét t1=tBCD, t2=tACD, t3=tABD és t4=tABC-vel.

Legyen a beírt gömb középpontja O. A tetraéder térfogata megegyezik a BCDO, ACDO, ABDO és ABCO tetraéderek térfogatának összegével. Mindegyik kis tetraéder egyik lapja az ABCD tetraéderrel mindig közös, a hozzá tartozó magasság pedig r, tehát

V_{ABCD} =V_{BCDO}+V_{ACDO}+V_{ABDO}+V_{ABCO} =\frac{r}3(t_1+t_2+t_3+t_4). (1)

Tegyük fel, hogy az O1 középpontú, r1 sugarú gömb az ábra szerint helyezkedik el. Az ABCD tetraéder térfogatát számítsuk ki a lapok és az O1 pont által meghatározott tetraéderek segítségével. Az ábrán látható elrendezésben

V_{ABCD} = V_{BCDO_1}+V_{ABCO_1}-V_{ACDO_1}-V_{ABDO_1} = \frac{r_1}{3}\big(t_1+t_4-t_2-t_3\big).

Ha a gömb nem az AD, hanem a BC élnél van, akkor az előjelek éppen fordítva állnak. Mindkét esetben igaz, hogy

V_{ABCD}= \frac{r_1}{3}\big|t_1+t_4-t_2-t_3\big|. (2)

Az (1) és (2) egyenletekből

\frac{r}{r_1}=\frac{|t_1+t_4-t_2-t_3|}{t_1+t_2+t_3+t_4}.

A betűzés alkalmas megválasztásával

\frac{r}{r_2}=\frac{|t_1+t_2-t_3-t_4|}{t_1+t_2+t_3+t_4}

és

\frac{r}{r_3}=\frac{|t_1+t_3-t_2-t_4|}{t_1+t_2+t_3+t_4}.

A szimmetria miatt feltételezhetjük, hogy t1\let2\let3\let4. Ha t1+t4>t2+t3, akkor

\frac{r}{r_1}+\frac{r}{r_2}+\frac{r}{r_3} = \frac{(t_1+t_4-t_2-t_3)+(t_3+t_4-t_2-t_1)+(t_2+t_4-t_1-t_3) }{t_1+t_2+t_3+t_4}=

= \frac{-t_1-t_2-t_3+3t_4}{t_1+t_2+t_3+t_4} < \frac{-t_1-t_2-t_3+t_4+2(t_1+t_2+t_3)}{t_1+t_2+t_3+t_4}=1,

figyelembe véve, hogy t4<t1+t2+t3.

Ha pedig t1+t4<t2+t3, akkor

\frac{r}{r_1}+\frac{r}{r_2}+\frac{r}{r_3} = \frac{(t_2+t_3-t_1-t_4)+(t_3+t_4-t_2-t_1)+(t_2+t_4-t_1-t_3) }{t_1+t_2+t_3+t_4}= \frac{-3t_1+t_2+t_3+t_4}{t_1+t_2+t_3+t_4}<1.

Mindkét esetben igaz tehát, hogy

\frac{r}{r_1}+\frac{r}{r_2}+\frac{r}{r_3} <1.

Ebből az állítás a számtani-harmonikus közepek közötti egyenlőtlenség miatt azonnal következik.

Statistics:

13 students sent a solution.
5 points:Erdélyi Márton, Estélyi István, Fischer Richárd, Gyenizse Gergő, Hujter Bálint, Jankó Zsuzsanna, Kisfaludi-Bak Sándor, Kónya 495 Gábor, Mészáros Gábor, Nagy 224 Csaba, Paulin Roland, Sümegi Károly.
4 points:Tomon István.

Problems in Mathematics of KöMaL, February 2006