 Problem A. 394. (February 2006)
Problem A. 394. (February 2006)
A. 394. Let a1,a2,...,aN be nonnegative reals, not all 0. Prove that there exists a sequence 1=n0<n1<...<nk=N+1 of integers such that
n1an0+n2an1+...+nkank-1<3(a1+a2+...+aN).
(5 pont)
Deadline expired on March 16, 2006.
Solution. Define aN+2+aN+3=...=0 as well and look for an infinite sequence 1=n0<n1<... of integers for which
Define the function f:[1,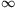 )
)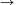 R such that f(x)=f([x]).
R such that f(x)=f([x]).
The required sequence is constructed randomly. Take a random variable t [0,1] of uniform distribution. Set n0=1 and
[0,1] of uniform distribution. Set n0=1 and for i=1,2,.... Then
The value of n1 is 2,3,4 or 5 if ,
,
, or
, respectively. Therefore
and
There always exists a sequence 1=n0<n1<...<nk=N+1 such that
n1an0+n2an1+...+nkank-1<3a1+e(a2+a3+...+aN).
Statistics:
3 students sent a solution. 5 points: Erdélyi Márton, Paulin Roland. 0 point: 1 student.
Problems in Mathematics of KöMaL, February 2006
