 Problem A. 396. (March 2006)
Problem A. 396. (March 2006)
A. 396. The elements of families and
are finite sets, each having at most n elements. Suppose that for an arbitrary finite set F there exist
and
such that X
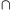 Y
Y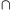 F=Ø. Prove that there exist
F=Ø. Prove that there exist and
such that X
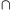 Y=Ø.
Y=Ø.
(5 pont)
Deadline expired on April 18, 2006.
Statistics:
6 students sent a solution. 5 points: Erdélyi Márton, Gyenizse Gergő, Nagy 224 Csaba, Paulin Roland. 3 points: 1 student. 2 points: 1 student.
Problems in Mathematics of KöMaL, March 2006
