 Problem A. 398. (April 2006)
Problem A. 398. (April 2006)
A. 398. Given a circle k in the plane and a line  lying outside k. Moreover, a point O is given on the circle. Define the binary operator + on the points of k as follows. For arbitrary points X and Y, denote by MXY the intersection point of lines XY and
lying outside k. Moreover, a point O is given on the circle. Define the binary operator + on the points of k as follows. For arbitrary points X and Y, denote by MXY the intersection point of lines XY and  . (If X=Y then take the tangent. If the lines are parallel then MXY is the ideal point.) Construct the second intersection of OMXY and k. (If the line is the tangent at O then also the second intersection is O.) Denote this point by X+Y (see the figure).
. (If X=Y then take the tangent. If the lines are parallel then MXY is the ideal point.) Construct the second intersection of OMXY and k. (If the line is the tangent at O then also the second intersection is O.) Denote this point by X+Y (see the figure).
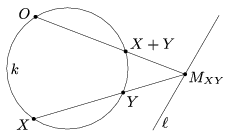
Show that operation + can be extended to the union of k,  and the ideal point of
and the ideal point of  such that the points with this operation form an Abelian group with the unity O; i.e. the operation has the following properties:
such that the points with this operation form an Abelian group with the unity O; i.e. the operation has the following properties:
a) (X+Y)+Z=X+(Y+Z) for all points X, Y, Z;
b) X+Y=Y+X for all points X, Y;
c) X+O=X for all points X;
d) For an arbitrary point X there exists a point Y such that X+Y=O.
(5 pont)
Deadline expired on May 18, 2006.
Statistics:
9 students sent a solution. 5 points: Jankó Zsuzsanna, Kisfaludi-Bak Sándor, Nagy 224 Csaba, Paulin Roland, Tomon István. 3 points: 1 student. 1 point: 2 students. 0 point: 1 student.
Problems in Mathematics of KöMaL, April 2006
