 Problem A. 404. (September 2006)
Problem A. 404. (September 2006)
A. 404. The vertices of a regular 2n-gon are . Call a diagonal ViVj even if i and j have the same parity. Dissect the polygon into triangles arbitrarily drawing 2n-3 nonintersecting diagonals. The following operation is allowed on this dissection: Choose two vertices, Vi and Vj, which are either consecutive or they are connected by a diagonal used for the dissection. Then, on one side of the line ViVj replace each diagonal by its mirror image through the perpendicular bisector of ViVj (see the figure). Prove that, starting from an arbitrary dissection and applying this operation several times, it can be achieved that all even diagonals used for the dissection connect only vertices of even indices.
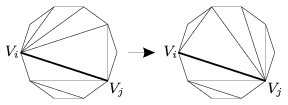
(Based on the sixth problem of the 47th IMO, Slovenia)
(5 pont)
Deadline expired on October 16, 2006.
Statistics:
21 students sent a solution. 5 points: Dobribán Edgár, Gyürke Csaba, Hujter Bálint, Károlyi Márton, Kisfaludi-Bak Sándor, Korándi Dániel, Kornis Kristóf, Lovász László Miklós, Nagy 224 Csaba, Nagy 235 János, Nagy 314 Dániel, Szűcs 003 Gábor, Tomon István, Varga 171 László. 4 points: Dudás László, Fischer Richárd. 3 points: 2 students. 1 point: 1 student. 0 point: 1 student. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, September 2006
