Problem A. 428. (May 2007)

A. 428. Given a convex lattice polygon such that both x- and y-coordinates of each vertex lie in the interval [0,n]. Show that the number of vertices is less than 100n^2/3.

(5 pont)

Deadline expired on June 15, 2007.

Solution. The number of vertices is trivially at most 4n, so we can assume that n $\ge$ 5⁶ and the number of vertices is at least 5⁴.

Let the side vectors of the polygon be (in counterclockwise order) v₁,v₂,...,v_k, where k $\ge$ 5⁴ is the number of vertices. Since the perimeter of the convex polygon cannot be greater than the perimeter of the square containing it,

$\sum_{i=1}^k|v_k| \le 4n.$

(1)

Sort the integer vectors in the plane by their lengths: $u_0,u_1,u_2,\ldots$ , ahol 0=|u₀|<|u₁| $\le$ |u₂| $\le$ |u₃| $\le$ ....

For an arbitrary positive integer m, consider the vectors u₀,...,u_m. Drawing a unit square around their end-points, these squares do not overlap and they are contained in a circle of radius |u_n|+1. Therefore m+1<(|v_m|+1)²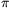 $\pi$ , and

$|v_m| > \sqrt{\frac{m+1}\pi} -1 > \frac{\sqrt{m}}2-1.$

Substituting into (1),

$4n \ge \sum_{i=1}^k |v_i| \ge \sum_{i=1}^k |u_i| \ge \sum_{i=1}^k \left(\frac{\sqrt{i}}2-1\right) >\frac13k^{3/2}-k \ge \frac13k^{2/3} - \frac1{5^2}k^{3/2} > \frac14k^{3/2}.$

Hence,

k<(16n)^2/3<100n^2/3.

Statistics:

8 students sent a solution.

5 points: Gyenizse Gergő, Kónya 495 Gábor, Lovász László Miklós, Nagy 224 Csaba, Nagy 235 János, Nagy 314 Dániel, Tomon István.

Unfair, not evaluated: 1 solutions.

Problems in Mathematics of KöMaL, May 2007

8 students sent a solution.
5 points:	Gyenizse Gergő, Kónya 495 Gábor, Lovász László Miklós, Nagy 224 Csaba, Nagy 235 János, Nagy 314 Dániel, Tomon István.
Unfair, not evaluated:	1 solutions.

Already signed up?
New to KöMaL?