 Problem A. 430. (May 2007)
Problem A. 430. (May 2007)
A. 430. Let n 2 and let
2 and let be arbitrary complex numbers with absolute values at most 1 and let
f(x)=(x-u1)(x-u2)...(x-un).
Prove that polynomial f'(x) has a root with a non-negative real part.
(5 pont)
Deadline expired on June 15, 2007.
Solution. If 1 is a multiple root of f then f'(1)=0 and the statement becomes trivial. So we assume that u2,...,un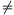 1.
1.
Let the roots of f'(x) be v1,v2...,vn-1, and consider the polynomial g(x)=f(1-x)=a1x+a2x2+...+anxn.
The nonzero roots of g(x) are 1-u2,...,1-un. From the Viéta-formulas we obtain
The roots of polynomial f'(1-x)=-g'(x)=-a1-2a2x-...-nanxn-1 are ; from the Viéta formulas again,
Combining the two equations,
For every k, the number uk lies in the unit disc (or on its boundary), and 1-uk lies in the circle with center 1 and unit radius (or on its boundary). The operation of taking reciprocals can be considered as the combination of an inversion from pole 0 and mirroring over the real axis. Hence lies in the half plane
, i.e.
.
Summing up these inequalities,
so at least one lies in the half plane
.
Repeating the same geometric steps backwards,
Statistics:
3 students sent a solution. 5 points: Tomon István. 4 points: Nagy 235 János. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, May 2007
