Problem A. 431. (September 2007)

A. 431. Triangle ABC is not isosceles. The incenter is I, the excenter is O. The incircle touches the sides BC, CA, AB at points D, E, F, respectively. Lines FD and AC intersect at P, lines DE and AB intersect at Q. The midpoints of segments EP amd FQ are M and N, respectively. Prove that MN and OI are perpendicular.

(Chinese Mathematical Olympiad, 2007)

(5 pont)

Deadline expired on October 15, 2007.

Solution. We prove that MN is the radical line of the incircle and the circumcircle.

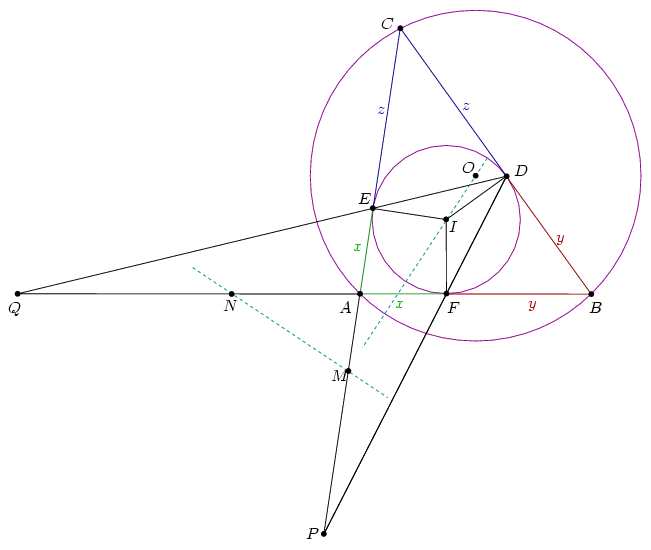
Let AE=AF=x, BD=BF=y and CD=CE=z. Denote the signed distance QA by u; let u be positive if the direction of QA matches the direction of AB. From Menelaus' theorem

$\frac{AQ}{QB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = -1,$

$\frac{-u}{u+x+y} \cdot \frac{y}{z} \cdot \frac{z}{x} = -1,$

$u = \frac{x(x+y)}{y-x}.$

Then $QF = QA+AF = u+x = \frac{2xy}{y-x}$ , $NF = \frac12QF = \frac{xy}{y-x}$ , $NA = NF - AF = \frac{xy}{y-x} - x = \frac{y^2}{y-x}$ and $NB = NF +FB = \frac{xy}{y-x} + y = \frac{x^2}{y-x}$ . Since

$NF^2 = NA \cdot NB = \frac{x^2y^2}{(y-x)^2},$

the powers of point N with respect to the incircle and the circumcircle match, so N lies on the radical line.

It can be obtained similarly that M lies on the radical line of the two circles. So MN itself is the radical line which is perpendicular to the central line OI.

Statistics:

10 students sent a solution.

5 points: Blázsik Zoltán, Gombor Tamás, Korándi Dániel, Lovász László Miklós, Nagy 235 János, Nagy 314 Dániel, Szűcs Gergely, Tomon István, Tuan Nhat Le, Wolosz János.

Problems in Mathematics of KöMaL, September 2007

10 students sent a solution.
5 points:	Blázsik Zoltán, Gombor Tamás, Korándi Dániel, Lovász László Miklós, Nagy 235 János, Nagy 314 Dániel, Szűcs Gergely, Tomon István, Tuan Nhat Le, Wolosz János.

Already signed up?
New to KöMaL?