 Problem A. 438. (November 2007)
Problem A. 438. (November 2007)
A. 438. On the circumcircle of the equilateral triangle ABC, choose an arbitrary point P on arc AB. Mark the points Q and R on arc BC and the points S and T on arc CA for which AP=BQ=CR=CS=AT holds. Let lines BQ and PR meet at U and let lines AS and PT meet at V. Finally, let lines AU and BV meet at W. Show that each two of lines AU, BV and PW enclose an angle of 60o.
(5 pont)
Deadline expired on December 17, 2007.
Solution (sketch). Triangles APV and PBA are similar since  VAP=
VAP= SAP=
SAP= APB=
APB= PBQ=
PBQ= PBU=120o and
PBU=120o and  APV=
APV= PBA.
PBA.
Let 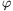 be the rotated homothety which transforms triangle APV into triangle PBA, i.e.
be the rotated homothety which transforms triangle APV into triangle PBA, i.e. 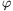 (V)=A,
(V)=A, 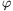 (A)=P and
(A)=P and 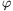 (P)=B. The angle between vectors AP and PB is 60o, so the angle of rotation is 60o.
(P)=B. The angle between vectors AP and PB is 60o, so the angle of rotation is 60o.
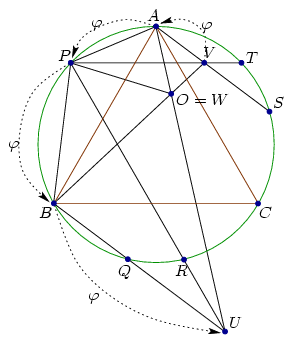
The image of line PB is BQ, because  (PB) passes through
(PB) passes through  (P)=B and its direction matches the direction of BP (since
(P)=B and its direction matches the direction of BP (since  PBQ=120o). It can be obtained similarly that
PBQ=120o). It can be obtained similarly that  (AB)=PR. Then
(AB)=PR. Then
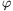 (B)=
(B)=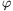 (PB
(PB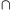 AB)=
AB)=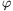 (PB)
(PB)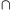
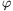 (AB)=BQ
(AB)=BQ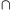 PR=U.
PR=U.
Therefore transformation 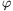 moves V to A, A to P, P to B, and B to U.
moves V to A, A to P, P to B, and B to U.
Let W be the homothety center. Then AOV =POA
=POA =BOP
=BOP =UOB
=UOB =60o. So O=W and the lines VW, AW, PW, BW and UW enclose angles of 60o.
=60o. So O=W and the lines VW, AW, PW, BW and UW enclose angles of 60o.
Statistics:
9 students sent a solution. 5 points: Huszár Kristóf, Korándi Dániel, Kornis Kristóf, Lovász László Miklós, Nagy 235 János, Nagy 314 Dániel, Tomon István, Wolosz János. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, November 2007
