 |
Az A. 440. feladat (2007. december) |
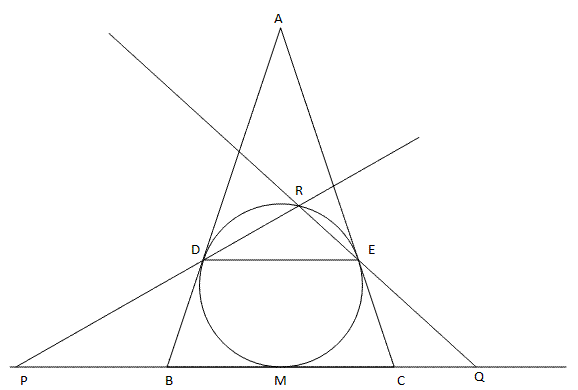
A. 440. Adott az ABC egyenlő szárú háromszög, amelyben a BC alap felezőpontja M, a D és E pontok pedig az AB, illetve AC szárak belső pontjai úgy, hogy DE párhuzamos BC-vel.
A BC oldal B-n, illetve C-n túli meghosszabbításán vegyük fel a P és Q pontokat úgy, hogy
teljesüljön. A PD és QE egyenesek metszéspontja legyen R. Mi az így kapható R pontok mértani helye?
(5 pont)
A beküldési határidő 2008. január 15-én LEJÁRT.
Megoldás (Lovász László Miklós megoldása). Legyen MB=MC=x, BP=p, CQ=q. Mivel P a B-n túli meghosszabbításon van, Q a C-n túlin, MP=MB+BP, és MQ=MC+CQ. Ekkor a megadott feltételt felírhatjuk úgy, hogy . A nevezőkkel ha felszorzunk (egyik se lehet nulla), azt kapjuk, hogy ez ekvivalens azzal, hogy x2+xq+x2+xp=x2+xq+xp+pq. Ezt leegyszerűsítve: x2=pq, vagyis
Nyilván BD=CE. Nézzük először azt az esetet, amikor BD=MB Ekkor . Legyen ABC
 =
= . Ekkor nyilván ACB
. Ekkor nyilván ACB =
= Ebből PBD
Ebből PBD =180o-
=180o- =ECQ
=ECQ . Tehát a PBD és ECQ háromszögek hasonlók. Mivel DE||BC, RED
. Tehát a PBD és ECQ háromszögek hasonlók. Mivel DE||BC, RED =CQE
=CQE =BDP
=BDP , és RDE
, és RDE =DPB
=DPB . Tehát a DRE háromszög is hasonló a PBD háromszöghöz. Ebből DRE
. Tehát a DRE háromszög is hasonló a PBD háromszöghöz. Ebből DRE =180o-
=180o- . Vagyis a DRE szög állandó, így a DE fölötti, 180o-
. Vagyis a DRE szög állandó, így a DE fölötti, 180o- szögű látóköríven van. (Nyilván R DE "fölött" van, mert P és Q BC-nek a B illetve C-n túli meghosszabbításán van.) Tehát egy állandó körön van. RDE
szögű látóköríven van. (Nyilván R DE "fölött" van, mert P és Q BC-nek a B illetve C-n túli meghosszabbításán van.) Tehát egy állandó körön van. RDE +DER
+DER =
= , tehát mivel DEA
, tehát mivel DEA =BCA
=BCA =
= , RDE
, RDE =REA
=REA . Tehát ha nézzük az RDE körülírt körét, ezt az AE egyenes érinti. Hasonló módon az AD egyenes is érinti ezt a kört. Viszont mivel AD=AE, BD=BM, CM=CE, ez pont a beírt kör lesz. Tehát azt kaptunk, hogy ebben az esetben az ABC beírt körének DE "fölötti", vagyis BC-vel ellentétes oldalán lévő részén van. Nyilván minden ilyen pontot megkapunk, mert ha választunk rajta egy pontot, azt összekötjük D és E-vel, és a hosszabításaikat elnevezzük P és Q-nak, akkor azok jók lesznek, csak ezt a gondolatmenetet meg kell fordítani.
. Tehát ha nézzük az RDE körülírt körét, ezt az AE egyenes érinti. Hasonló módon az AD egyenes is érinti ezt a kört. Viszont mivel AD=AE, BD=BM, CM=CE, ez pont a beírt kör lesz. Tehát azt kaptunk, hogy ebben az esetben az ABC beírt körének DE "fölötti", vagyis BC-vel ellentétes oldalán lévő részén van. Nyilván minden ilyen pontot megkapunk, mert ha választunk rajta egy pontot, azt összekötjük D és E-vel, és a hosszabításaikat elnevezzük P és Q-nak, akkor azok jók lesznek, csak ezt a gondolatmenetet meg kell fordítani.

Nézzük azt az esetet, amikor BD BM Ekkor létezik olyan affinitás, amelyben csak függőlegesen, vagyis BC-re merőlegesen mozgatjuk a pontokat, és olyan arányban, hogy BD egyenlő legyen BM-el. Ez az affinitás a P, B, M, C, és Q pontokon nem változtat, vagyis ugyanazokat a P és Q pontokat kapjuk. Az affinitás egyenest egyenesbe visz, tehát az R pontokkal is ugyanaz történik. Vagyis az affinitás után az ilyen R pontok mértani helye a beírt kör. Az affinitás során kört csak ellipszisből kaphattunk. Tehát eredetileg az alakzat ellipszis volt. Az affinitás azon nem változtat, hogy ez érinti az egyeneseket a D, E, és M pontokban. Tehát az eredeti ábrában az ilyen R pontok mértani helye azok, amelyek a háromszögben lévő, D, E, és M pontokban érintő ellipszis, és persze ennek DE BC-vel ellentétes oldalán lévő része.
BM Ekkor létezik olyan affinitás, amelyben csak függőlegesen, vagyis BC-re merőlegesen mozgatjuk a pontokat, és olyan arányban, hogy BD egyenlő legyen BM-el. Ez az affinitás a P, B, M, C, és Q pontokon nem változtat, vagyis ugyanazokat a P és Q pontokat kapjuk. Az affinitás egyenest egyenesbe visz, tehát az R pontokkal is ugyanaz történik. Vagyis az affinitás után az ilyen R pontok mértani helye a beírt kör. Az affinitás során kört csak ellipszisből kaphattunk. Tehát eredetileg az alakzat ellipszis volt. Az affinitás azon nem változtat, hogy ez érinti az egyeneseket a D, E, és M pontokban. Tehát az eredeti ábrában az ilyen R pontok mértani helye azok, amelyek a háromszögben lévő, D, E, és M pontokban érintő ellipszis, és persze ennek DE BC-vel ellentétes oldalán lévő része.
Megjegyzés. Nem tekintettük teljesnek azokat a megoldásokat, amelyek az ellipszisről nem mutatták meg, hogy érintik az AB és AC oldalakat, illetve azt, hogy a elipszis alkalmas affinitás hatására a beírt körbe megy át.
Két versenyző az ellipszis egyenletét írta fel a kelleténél bonyolultabban, egy pedig az ellipszis megadásához egy további, mesterséges pontot használt. Mivel ők hárman a keresett ellipszis fenti, lényeges geometriai tujdonságát nem fedezték fel, 4 pontot kaptak.
Statisztika:
8 dolgozat érkezett. 5 pontot kapott: Blázsik Zoltán, Korándi Dániel, Lovász László Miklós, Nagy 314 Dániel. 4 pontot kapott: Nagy 235 János, Tomon István, Wolosz János. Nem versenyszerű: 1 dolgozat.
A KöMaL 2007. decemberi matematika feladatai

