 Problem A. 456. (May 2008)
Problem A. 456. (May 2008)
A. 456. The point D lies in the triangle ABC such that the circles inscribed in triangles ABD, BCD, and CAD pairwise touch each other. On lines BC, CA, AB, AD, BD, CD, denote the touching points by A1, B1, C1, A2, B2, C2, respectively. Let lines B1C2 and B2C1 meet at E, and let lines A1C2 and A2C1 meet at F. Show that the lines AF, BE, and C1D are concurrent.
(5 pont)
Deadline expired on June 16, 2008.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A megoldás során többször használjuk az következő, jól ismert tételt:
Bármely három különböző kör 6 hasonlósági középpontja négy egyenesen helyezkedik el, nevezetesen
-- egy egyenesre esik a három külső hasonlósági középpont;
-- egy egyenesre esik bármelyik két belső és a harmadik körpárhoz tartozó hasonlósági középpont.
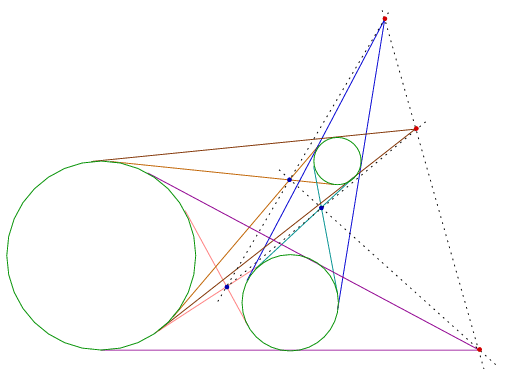
Jelöljük a \(\displaystyle ABC\), \(\displaystyle BCD\), \(\displaystyle CAD\), \(\displaystyle ABD\) háromszögek beírt körét rendre \(\displaystyle i\), \(\displaystyle \omega_A\), \(\displaystyle \omega_B\), \(\displaystyle \omega_C\)-vel.
Az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), illetve \(\displaystyle D\) pontokból a \(\displaystyle \omega_A\), \(\displaystyle \omega_B\) és \(\displaystyle \omega_C\) körökhöz húzott érintő szakaszok egyenlő hosszúak, ezért
\(\displaystyle AB_1=AA_2=AC_1\), \(\displaystyle BA_1=BB_2=BC_1\), \(\displaystyle CA_1=CC_2=CB_1\) és \(\displaystyle DA_2=DB_2=D,C_2\).
Az \(\displaystyle AB_1=AC_1\), \(\displaystyle BA_1=BC_1\) és \(\displaystyle CA_1=CB_1\) összefüggések teljesülnek az \(\displaystyle ABC\) háromszögbe írt kör érintési pontjaira, és egyértelműen meghatározzák az \(\displaystyle A_1\), \(\displaystyle B_1\), és \(\displaystyle C_1\) pontokat. Tehát, a \(\displaystyle i\) beirt kör az \(\displaystyle A_1\), \(\displaystyle B_1\) és \(\displaystyle C_1\) pontokban érinti az oldalakat.
Az \(\displaystyle ADBC\) (konkáv) négyszög érintőnégyszög, mert a szemközti oldalainak össege megegyezik:
\(\displaystyle AD+BC = (AA_2+DA_2)+(BA_1+CA_1) = (DB_2+BB_2)+(CB_1+AB_1) = AC+D. \)
Létezik tehát egy \(\displaystyle \Omega_C\) kör, ami érinti az \(\displaystyle AC\) és \(\displaystyle BC\) oldalat, valamint az \(\displaystyle AD\) és \(\displaystyle BD\) oldalak meghosszabítását.
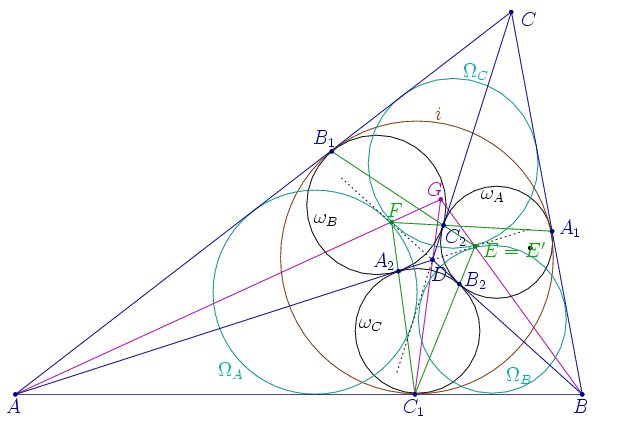
Legyen az \(\displaystyle i\) és \(\displaystyle \omega_A\) körök belső hasonlósági pontja \(\displaystyle E'\). Az \(\displaystyle i\) és az \(\displaystyle \omega_B\) külső hasonlósági pontja \(\displaystyle B_1\), az \(\displaystyle \omega_A\) és az \(\displaystyle \omega_B\) belső hasonlósági pontja pedig \(\displaystyle C_2\). Ezért az \(\displaystyle B_1\), \(\displaystyle C_2\) és \(\displaystyle E'\) pontok egy egyenesen vannak.
Hasonlóképpen \(\displaystyle C_1\), az \(\displaystyle i\) és az \(\displaystyle \omega_C\) külső hasonlósági pontja, valamint \(\displaystyle B_2\), az \(\displaystyle \omega_A\) és az \(\displaystyle \omega_C\) belső hasonlósági pontja is egy egyenesen van \(\displaystyle E'\)-vel. Tehát \(\displaystyle E'=E\).
Az \(\displaystyle A\) és \(\displaystyle B\) pontok szerepének felcserélésével kapjuk, hogy az \(\displaystyle F\) pont az \(\displaystyle i\) és \(\displaystyle \omega_B\) körök belső hasonlósági pontja.
Végül, legyen \(\displaystyle G\) az \(\displaystyle i\) és \(\displaystyle \Omega_C\) körök belső hasonlósági pontja. Megmutatjuk, hogy az az \(\displaystyle AF\), \(\displaystyle BE\) és \(\displaystyle C_1D\) egyenesek mindegyike átmegy \(\displaystyle G\)-n.
Mivel \(\displaystyle \omega_B\) és \(\displaystyle \Omega_C\) külső hasonlósági pontja \(\displaystyle A\), illetve \(\displaystyle \omega_B\) és \(\displaystyle i\) belső hasonlósági pontja \(\displaystyle F\), az \(\displaystyle AF\) egyenes átmegy \(\displaystyle G\)-n.
Mivel \(\displaystyle \omega_A\) és \(\displaystyle \Omega_C\) külső hasonlósági pontja \(\displaystyle B\), illetve \(\displaystyle \omega_A\) és \(\displaystyle i\) belső hasonlósági pontja \(\displaystyle E\), a \(\displaystyle BE\) egyenes átmegy \(\displaystyle G\)-n.
Mivel \(\displaystyle \omega_C\) és \(\displaystyle i\) külső hasonlósági pontja \(\displaystyle C_1\), illetve \(\displaystyle \omega_C\) és \(\displaystyle \Omega_A\) belső hasonlósági pontja \(\displaystyle D\), a \(\displaystyle C_1D\) egyenes is átmegy \(\displaystyle G\)-n.
Megjegyzés. Az ábrából sejthető, hogy az \(\displaystyle AD\) és \(\displaystyle BD\) egyenesek is átmennek az \(\displaystyle E\), illetve \(\displaystyle F\) pontokon.
Legyen \(\displaystyle \Omega_A\) a \(\displaystyle CABD\) érintőnégyszög beírt köre. Az \(\displaystyle i\) és \(\displaystyle \Omega_A\) körök külső hasonlósági pontja \(\displaystyle A\), az \(\displaystyle \omega_A\) és \(\displaystyle \Omega_A\) körök belső hasonlósági pontja \(\displaystyle D\), az \(\displaystyle \omega_A\) és \(\displaystyle i\) körök belső hasonlósági pontja pedig \(\displaystyle E\), Ezért az \(\displaystyle A\), \(\displaystyle D\) és \(\displaystyle E\) pontok, és teljesen hasonlóan a \(\displaystyle B\), \(\displaystyle D\) és \(\displaystyle F\) pontok is egy egyenesen vannak.
Statistics:
4 students sent a solution. 5 points: Lovász László Miklós, Nagy 235 János, Tomon István. 0 point: 1 student.
Problems in Mathematics of KöMaL, May 2008
