 Problem A. 464. (November 2008)
Problem A. 464. (November 2008)
A. 464. Let H a set and denote by P(H) the family of all subsets of H. Suppose that f and g are P(H)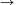 P(H) maps such that f(X)
P(H) maps such that f(X) f(Y)
f(Y) H and g(X)
H and g(X) g(Y)
g(Y) H whenever X
H whenever X Y
Y H. Prove that there exist sets A,B
H. Prove that there exist sets A,B H for which f(A)=H\B and g(B)=H\A.
H for which f(A)=H\B and g(B)=H\A.
(5 pont)
Deadline expired on December 15, 2008.
Solution. For every X H, let h(X)=H\g(H\f(X)). Our goal is to construct a set A
H, let h(X)=H\g(H\f(X)). Our goal is to construct a set A H for which h(A)=A,
H for which h(A)=A,
The function the function h s nondecreasing, i.e. h(X) h(Y) whenever X
h(Y) whenever X Y
Y H.
H.
Call a set X H "nice" if X
H "nice" if X h(X) and let A be the union of all nice sets:
h(X) and let A be the union of all nice sets:
We will show that h(A)=A. Let A'=h(A).
For every nice set X we have X A and thus X
A and thus X h(X)
h(X) h(A). Then
h(A). Then
Therefore, the set A is nice, A h(A).
h(A).
Since h is nondecreasing, the set A' is nice as well; A'=h(A) h(A'). On the othe hand, A is the union of all nice sets, so A'=h(A) is a subset of A.
h(A'). On the othe hand, A is the union of all nice sets, so A'=h(A) is a subset of A.
Hence, A h(A) and h(A)
h(A) and h(A) A. Therefore A=h(A).
A. Therefore A=h(A).
Statistics:
9 students sent a solution. 5 points: Backhausz Tibor, Bodor Bertalan, Éles András, Tomon István, Tossenberger Anna. 2 points: 2 students. 0 point: 2 students.
Problems in Mathematics of KöMaL, November 2008
