Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation
Already signed up?
New to KöMaL?

Problem A. 465. (November 2008)

A. 465. Show that 6 does not divide \big[\big(\root3\of{28}-3\big)^{-n}\big] for any positive integer n.

(5 pont)

Deadline expired on December 15, 2008.

Solution (outline). From a3-b3=(a-b)(a2+ab+b2) we have

\big(\root3\of{28}-3\big)^{-1} = \big(\root3\of{28}\big)^2+\root3\of{28}\cdot3+3^2

and

\big(\root3\of{28}-3\big)^{-n} = \Big(\big(\root3\of{28}\big)^2+\root3\of{28}\cdot3+3^2\Big)^n= \sum_{k+l+m=n}\frac{n!}{k!l!m!} \big(\root3\of{28}\big)^{2k+l}3^{l+m2}.

Let \varepsilon=\cos\frac{2\pi}3+i\cdot\sin\frac{2\pi}3 and consider the number

S= \Big(\big(\root3\of{28}\big)^2+\root3\of{28}\cdot3+3^2\Big)^n + \Big(\big(\root3\of{28}\varepsilon\big)^2+ \big(\root3\of{28}\varepsilon\big)\cdot3+3^2\Big)^n + \Big(\big(\root3\of{28}\varepsilon^2\big)^2+ \big(\root3\of{28}\varepsilon^2\big)\cdot3+3^2\Big)^n =

= \sum_{k+l+m=n}\frac{n!}{k!l!m!} \big(\root3\of{28}\big)^{2k+l}3^{l+m2} \big(1+\varepsilon^{2k+l}+\varepsilon^{4k+2}\big).

Whenever 3 does not divide 2k+1 and 4k+2, the sum between the last parentheses is 1+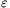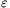\varepsilon+\varepsilon2=0.

In those cases when 3 divides 2k+1 and 4k+2, the value of the last factor is 3. Such terms are integers, and the only odd value is the l;ast one when k=l=0 ann m=n. Hence, s is an integer and S\equiv3 (mod 6).

It is easy to check that \Big|\big(\root3\of{28}\varepsilon\big)^2+ \big(\root3\of{28}\varepsilon\big)\cdot3+3^2\Big|<1 and \Big|\big(\root3\of{28}\varepsilon^2\big)^2+ \big(\root3\of{28}\varepsilon^2\big)\cdot3+3^2\Big|<1.

(E.g. these numbers are conjucates and

\Big(\big(\root3\of{28}\big)^2+\root3\of{28}\cdot3+3^2\Big)\cdot \Big(\big(\root3\of{28}\varepsilon\big)^2+ \big(\root3\of{28}\varepsilon\big)\cdot3+3^2\Big)\cdot \Big(\big(\root3\of{28}\varepsilon^2\big)^2+ \big(\root3\of{28}\varepsilon^2\big)\cdot3+3^2\Big) =

= \frac{1}{\big(\root3\of{28}-3\big)\big(\root3\of{28}\varepsilon-3\big)\big(\root3\of{28}\varepsilon^2-3\big)} =\frac{1}{28-3^3}=1.

Therefore, the two latter terms in S are of absolute value less than 1.

Statistics:

5 students sent a solution.
5 points:Nagy 235 János, Nagy 314 Dániel, Nagy 648 Donát, Tomon István.
0 point:1 student.

Problems in Mathematics of KöMaL, November 2008