 Problem A. 468. (December 2008)
Problem A. 468. (December 2008)
A. 468. We are given two triangles. Their side lengths are a,b,c and A,B,C respectively, the areas are t and T, respectively. Prove that -a2A2+a2B2+a2C2+b2A2-b2B2+b2C2+c2A2+c2B2-c2C2 16tT.
16tT.
(5 pont)
Deadline expired on January 15, 2009.
Solution. Let  and
and 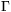 the two angles opposite to sides c and C, respectively. From the cosine law we have a2+b2-c2=2abcos
the two angles opposite to sides c and C, respectively. From the cosine law we have a2+b2-c2=2abcos  and A2+B2-C2=2ABsin
and A2+B2-C2=2ABsin 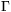 ; the two areas are
; the two areas are and
.
Substituing these quantities,
-a2A2+a2B2+a2C2+b2A2-b2B2+b2C2+c2A2+c2B2-c2C2-16tT=
=2a2B2+2A2b2-(a2+b2-c2)(A2+B2-C2)-16tT=
=2a2B2+2A2b2-4abABcos  cos
cos 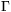 -4abABsin
-4abABsin  sin
sin 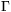 =
=
=2(aB-Ab)2+4abAB(1-cos ( -
-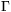 ))
)) 0.
0.
Statistics:
12 students sent a solution. 5 points: Blázsik Zoltán, Bodor Bertalan, Éles András, Márkus Bence, Nagy 235 János, Nagy 648 Donát, Somogyi Ákos, Tomon István, Tossenberger Anna, Varga 171 László, Wolosz János. 4 points: Backhausz Tibor.
Problems in Mathematics of KöMaL, December 2008
