Problem A. 495. (December 2009)

A. 495. In the acute triangle ABC we have $\angle$ BAC= $\alpha$ . The point D lies in the interior of the triangle, on the bisector of $\angle$ BAC, and points E and F lie on the sides AB and BC, respectively, such that $\angle$ BDC=2 $\alpha$ , $\angle$ AED=90^o+ $\frac{\alpha}{2}$ , and $\angle$ BEF= $\angle$ EBD. Determine the ratio BF:FC.

(5 pont)

Deadline expired on January 11, 2010.

Solution. Let G be the reflection of E through the bisector AD. Reflect point D through the lines AB and AC; denote the reflections by U and V, respectively. We have UE=DE=DG=VG.

From the deltoid AEDG we obtain $AEG\angle=AGE\angle=90^\circ-\frac\alpha2$ and $DEG\angle=DGE\angle=AED\angle-AEG\angle= \bigg(90^\circ+\frac\alpha2\bigg)- \bigg(90^\circ-\frac\alpha2\bigg) =\alpha$ .

Moreover, $BEU\angle=BED\angle=180^\circ-AED\angle=90^\circ-\frac\alpha2$ and $CGU\angle=CGD\angle=180^\circ-AGD\angle=90^\circ-\frac\alpha2$ .

Since BEU $\angle$ =AEG $\angle$ and CGV $\angle$ =AGE $\angle$ , the ponts U, E, G and V are collinear.

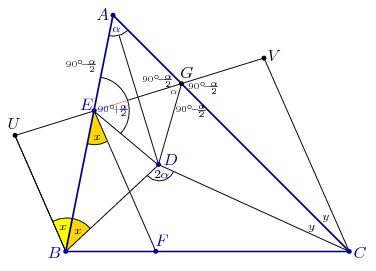
Leet BEF $\angle$ =BDE $\angle$ =EBU $\angle$ =x and CGF $\angle$ =CDG $\angle$ =GCV $\angle$ =z. From the quadrilateral ABDC and the triangle ABC, we have x+y=360^o- $\alpha$ -(360^o-2 $\alpha$ )= $\alpha$ and

UBC $\angle$ +BCV $\angle$ =(ABC $\angle$ +x)+(ACB $\angle$ +y)=180^o.

Therefore, the lines BU and CV are parallel. Due to EBU $\angle$ =VEF $\angle$ , also the line EF is parallel with them.

Hence,

$\frac{BF}{FC} = \frac{UE}{EV} = \frac{1}{2\cos\alpha + 1}.$

Statistics:

5 students sent a solution.

5 points: Bodor Bertalan, Éles András, Nagy 235 János, Nagy 648 Donát.

2 points: 1 student.

Problems in Mathematics of KöMaL, December 2009

5 students sent a solution.
5 points:	Bodor Bertalan, Éles András, Nagy 235 János, Nagy 648 Donát.
2 points:	1 student.

Already signed up?
New to KöMaL?