 Problem A. 496. (December 2009)
Problem A. 496. (December 2009)
A. 496. Let a1,a2,...,a2k be distinct integers and let M be a set of k integers not containing 0 and s=a1+a2+...+a2k. A grasshopper is to jump along the real axis, starting at the point 0 and making 2k jumps with lengths a1,a2,...,a2k in some order. If ai>0 then the grasshopper jumps to the right; while if ai<0 then the grasshopper jumps to the left, to the point in the distance |ai| in the respective steps. Prove that the order can be chosen in such a way that the grasshopper never lands on any point in M.
(5 pont)
Deadline expired on January 11, 2010.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Sn-nel fogjuk jelölni az (1,2,...,n) indexek permutációinak csoportját. Minden egyes 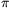
 Sn-re
Sn-re jelöli a
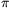 permutáció előjelét, ami páros permutációra +1, páratlan permutációra -1.
permutáció előjelét, ami páros permutációra +1, páratlan permutációra -1.
Legyen
| (1) |
és tekintsük a számot.
Ha , akkor létezik legalább egy olyan
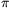
 S2k permutáció, amire
S2k permutáció, amire
Ez utóbbi viszont akkor és csak akkor nem 0, ha az ,
, ...,
számok különböznek az összes M-beli számtól; más szóval akkor, ha a szöcske végig tud ugrálni a 0,
,
, ...,
, ...,
, s számokon. Célunk tehát annak igazolása, hogy
.
A P polinom alternáló, vagyis bármelyik két változó felcserélésével a polinom (-1)-szeresét kapjuk, és ha bármelyik két változó helyére ugyanazt az értéket helyettesítjük, a polinom értéke 0 lesz. Jól ismert, hogy minden alternáló polinom, tehát P is, töbszöröse a
úgynevezett Vandermonde-polinomnak. A P foka legfeljebb k(2k-1), ami megegyezik a Vandermonde-polinom fokával. A P tehát konstansszorosa a Vandermonde-polinomnak:
(A (-1)k előjel egy kis magyarázatra szorul. A szorzatban a Vandermonde-polinom tagjai közül az x12k-1x22k-2...x2k-1 szerepel a legtöbbször; a Vandermonde-polinomban ennek a tagnak az együtthatója (-1)k.)
Észrevehetjük, hogy a P polinom, és vele együtt a ck szám egyáltalán nem függ az M halmaztól. Ezért ugyanazzal a ck konstanssal az is igaz, hogy
| (2) |
Az ugrásokat behelyettesítve,
Mvel az ugrások különbözőek,
. A feladat megoldásához már csak annyi hiányzik, hogy ck
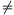 0, avagy, (1) jobboldala nem esik ki szőröstül-bőröstül.
0, avagy, (1) jobboldala nem esik ki szőröstül-bőröstül.
A ck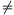 0 állításnál többet bizonyítunk.
0 állításnál többet bizonyítunk.
Definíció. Legyen tetszőleges u,v 0 egészekre
0 egészekre
| (3) |
Tetszőleges egészekre jelöljük
-nel x1d1...xndn együtthatóját a P(n,u,v) polinomban. Mivel a polinom alternáló,
| (4) |
Az egyszerűség kedvéért az együtthatót akkor is definiáljuk, ha di=di+1 valamelyik 1
 i<n indexre, vagy ha dn<0; ilyenkor
i<n indexre, vagy ha dn<0; ilyenkor .
1. lemma. n 2 esetén
2 esetén
(a) tetszőleges sorozatra
és
(b) tetszőleges sorozatra
Bizonyítás. Tekintsük a
polinomot.
A baloldalon a szorzatban nem szerepel az
változó. Ezért x1d1x2d2...xn-1dn-1 alakú tagot csak az olyan permutációkra kaphatunk, amikben
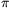 (n)=n. Az ilyen permutációkra összegezve pedig
(n)=n. Az ilyen permutációkra összegezve pedig
Tehát x1d1x2d2...xn-1dn-1 együtthatója a P(n,u,0) polinomban ugyanaz, mint a P(n-1,u,u) polinomban.
2. lemma. Ha v 1, akkor tetszőleges
1, akkor tetszőleges sorozatra
Bizonyítás. A P(n,u,v) definiója alapján
Az x1d1x2d2...xndn együtthatója a baloldalon , a jobboldalon az
polinomban pedig
.
3. lemma. Tetszőleges n 1, u,v
1, u,v 0 és
0 és egész számokra
Bizonyítás. Indukció. n=1 esetén P(1,u,v)(x1)=x1v, az egyetlen együttható pozitív. Innen, az 1. és 2. lemmát alkalmazva, triviális.
4. lemma. Legyenek n 1, u
1, u n/2 és v
n/2 és v 0 egészek. Ekkor
0 egészek. Ekkor minden olyan, egészekből álló
sorozatra, amelyben
és dn
 v.
v.
Bizonyítás. Teljes indukcióval bizonyítunk.
Az n=1 esetben P(1,u,v)(x1)=x1v, és az egyetlen együttható  (1,u,v)v=1>0. A továbbiakban feltételezzük, hogy n>1, és az állítás igaz minden olyan esetben, amikor
(1,u,v)v=1>0. A továbbiakban feltételezzük, hogy n>1, és az állítás igaz minden olyan esetben, amikor
(a) n-et kisebbre cseréljük, vagy pedig
(b) v értékét csökkentjük, miközben n értéke változatlan marad.
1. eset: v=0. A dn v feltétel miatt csak dn=0 lehetséges. Az 1. lemma szerint
v feltétel miatt csak dn=0 lehetséges. Az 1. lemma szerint
Az indukciós feltételt az (n',u',v')=(n-1,u,u) hármasra és az számokra alkalmazzuk.
Az feltétel teljesül, mert
.
Mivel v=dn=0,
Végül,
A lemma feltételei tehát mind teljesülnek, és .
2. eset: v>0. Az indukciós feltevést most az (n',u',v')=(n,u,v-1) hármasra alkalmazzuk, mert a 2. lemma szerint
A 3. lemma szerint a jobboldalon csupa nemnegatív szám áll; azt kell megmutatnunk, hogy van közöttük legalább egy pozitív is.
Mivel
létezik legalább egy olyan 1 i
i n index, amire di>n-i. Tekintsük az utolsó ilyen indexet. Ha i<n, akkor di-1>di+1; ha pedig i=n, akkor dn-1
n index, amire di>n-i. Tekintsük az utolsó ilyen indexet. Ha i<n, akkor di-1>di+1; ha pedig i=n, akkor dn-1 0.
0.
Alkalmazzuk az indukciós feltevést az számokra. Az i választásából következik, hogy
.
Az feltétel triviálisan teljesül.
Végül, d'n=max (dn-1,0) v-1 miatt az igaz, hogy d'n
v-1 miatt az igaz, hogy d'n v.
v.
Az indukciós feltevés tehát az számok közül legalább egyre alkalmazható.
Ezzel a Lemmát igazoltuk.
Következmény. ck>0 minden egyes pozitív egész k-ra.
Bizonyítás. Alkalmazzuk a 4. lemmát az n=2k, u=k, v=0, számokra. A lemma feltételei teljesülnek, ezért
Statistics:
2 students sent a solution. 4 points: Nagy 235 János. 3 points: 1 student.
Problems in Mathematics of KöMaL, December 2009
