Az A. 497. feladat (2010. január)

A. 497. Adott a síkon egy hegyesszögű ABC háromszög. A háromszög egy tetszőleges belső P pontjának a BC, CA és AB oldalakra eső vetületeit jelölje A₁, B₁, illetve C₁. A PAC₁, PC₁B, PBA₁, PA₁C, PCB₁ és PB₁A háromszögek beírt köreinek sugarai legyenek rendre $\varrho$ ₁, $\varrho$ ₂,..., $\varrho$ ₆.

Határozzuk meg azon P pontok mértani helyét, amelyekre

$\varrho$ ₁+ $\varrho$ ₃+ $\varrho$ ₅= $\varrho$ ₂+ $\varrho$ ₄+ $\varrho$ ₆.

Javasolta: Vígh Viktor (Szeged)

(5 pont)

A beküldési határidő 2010. február 10-én LEJÁRT.

Megoldásvázlat.

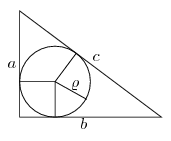
Felhasználjuk azt a jól ismert tényt, hogy ha egy derékszögű háromszög befogóinak hossza a és b, átfogója c, a beírt kör sugara pedig $\varho$ , akkor

$\varrho=\frac{a+b-c}{2}.$

(2)

(2) bizonyítása: Legyenek a háromszög csúcsai P,Q,R, a beírt kör középpontja I, az érintési pontok P₁,Q₁,R₁ az ábra szerint. Az IP₁Q₁R négyzet oldalainak hossza P₁R=Q₁R=IP₁=IQ₁= $\varrho$ , és a+b=(PQ₁+Q₁R)+(QP₁+P₁R)=(PQ₁+QP₁)+Q₁R+P₁R=(PR₁+QR₁)+ $\varrho$ + $\varrho$ =c+2 $\varrho$ .

Az (1) feltételbe behelyettesítve (2)-t,

$\varrho$ ₁+ $\varrho$ ₃+ $\varrho$ ₅- $\varrho$ ₂- $\varrho$ ₄- $\varrho$ ₆=

$= \frac{PC_1+AC_1-PA}{2} + \frac{PA_1+BA_1-PB}{2} + \frac{PB_1+CB_1-PC}{2} - ~ ~ ~$

$~ ~ ~ - \frac{PC_1+C_1B-PB}{2} - \frac{PA_1+A_1C-PC}{2} - \frac{PB_1+B_1A-PA}{2} =$

$= \frac{AC_1+BA_1+CB_1-C_1B-A_1C-B_1A}{2},$

vagyis (1) ekvivalens azzal, hogy

AC₁+BA₁+CB₁-C₁B-A₁C-B₁A=0.

(3)

Két ilyen pont a háromszögben például a körülírt kör középpontja (amikor AC₁=C₁B, BA₁=A₁C és CB₁=B₁A), illetve a beírt kör középpontja (amikor AC₁=B₁A, BA₁=C₁B és CB₁=A₁C).

Legyen az AB, BC, CA szakaszok felezőpontja rendre C₀, A₀ és B₀, a körülírt kör középpontja O, továbbá legyen ${\bf u}=\frac{\vec{AB}}{|AB|}$ , ${\bf v}=\frac{\vec{BC}}{|BC|}$ és ${\bf w}=\frac{\vec{CA}}{|CA|}$ .

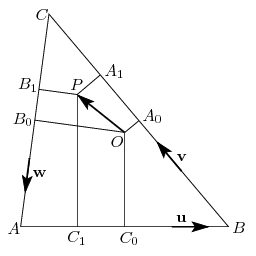
A $\vec{OP}$ vektornak az oldalakra eső előjeles vetületeit az u, v, w vektorokkal vett skaláris szorzatai adják meg:

$AC_1=AC_0+{\bf u}\cdot \vec{OP}, \qquad C_1B=C_0B-{\bf u}\cdot \vec{OP},$

$BA_1=BA_0+{\bf v}\cdot \vec{OP}, \qquad A_1C=A_0C-{\bf v}\cdot \vec{OP},$

$CB_1=CB_0+{\bf w}\cdot \vec{OP}, \qquad B_1A=B_0A-{\bf w}\cdot \vec{OP}.$

Tehát

AC₁+BA₁+CB₁-C₁B-A₁C-B₁A=

$= AC_0+BA_0+CB_0-C_0B-A_0C-B_0A + 2({\bf u}+{\bf v}+{\bf w})\cdot\vec{OP} =$

$= 2({\bf u}+{\bf v}+{\bf w})\cdot\vec{OP}.$

A (3) feltétel tehát ekvivalens azzal, hogy

$({\bf u}+{\bf v}+{\bf w})\cdot\vec{OP} = \bf0.$

(4)

Ha az ABC háromszög szabályos, akkor u+v+w=0. és (4) mindig teljesül.

Ha viszont az ABC háromszög nem szabályos, akkor u+v+w $\ne$ 0, és (4) az O-átmenő, a u+v+w vektorra merőleges egyenes pontjain teljesül. Ennek az egyenesnek ismerjük még egy pontját: a beírt kör középppontját, ami nem esik egybe O-val.

A keresett halmaz tehát:

- szabályos háromszög esetén a háromszög belseje;

- nem szabályos háromszög esetén a körülírt és a beírt kör középpontját összekötő egyenesnek a háromszög belsejébe eső szakasza.

Statisztika:

14 dolgozat érkezett.

5 pontot kapott: Bodor Bertalan, Éles András, Frankl Nóra, Mester Márton, Nagy 648 Donát, Nagy Balázs, Popper Dávid, Somogyi Ákos, Strenner Péter, Szabó 928 Attila, Weisz Ágoston.

4 pontot kapott: Frittmann Júlia, Nagy 235 János.

0 pontot kapott: 1 versenyző.

A KöMaL 2010. januári matematika feladatai

14 dolgozat érkezett.
5 pontot kapott:	Bodor Bertalan, Éles András, Frankl Nóra, Mester Márton, Nagy 648 Donát, Nagy Balázs, Popper Dávid, Somogyi Ákos, Strenner Péter, Szabó 928 Attila, Weisz Ágoston.
4 pontot kapott:	Frittmann Júlia, Nagy 235 János.
0 pontot kapott:	1 versenyző.

Már regisztráltál?
Új vendég vagy?