Problem A. 507. (April 2010)

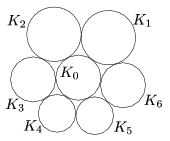
A. 507. The circles \(\displaystyle K_1,\dots,K_6\) are externally tangent to the circle \(\displaystyle K_0\) in this order. For each \(\displaystyle 1\le i\le 5\), the circles \(\displaystyle K_i\) and \(\displaystyle K_{i+1}\) are externally tangent to each other, and \(\displaystyle K_1\) and \(\displaystyle K_6\) are externally tangent to each other as well, according to the Figure. Denote by \(\displaystyle r_i\) the radius of \(\displaystyle K_i\) (\(\displaystyle 0\le i\le6\)). Prove that if \(\displaystyle r_1r_4=r_2r_5=r_3r_6=1\) then \(\displaystyle {r_0\le 1}\).

Proposed by: Balázs Strenner, Székesfehérvár

(5 pont)

Deadline expired on May 10, 2010.

Statistics:

2 students sent a solution.
4 points:	Nagy 648 Donát.
1 point:	1 student.

Problems in Mathematics of KöMaL, April 2010