Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation

Already signed up?
New to KöMaL?

Problem A. 517. (October 2010)

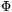A. 517. Let m $\ge$ 3 be a positive integer, and let $\Phi$ _m(x) be the mth cyclotomic polynomial, and denote by 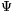$\Psi$ _m(x) the polynomial with integer coefficients for which $x^{\varphi(m)/2} \Psi_m\left(x+\frac1x\right) = \Phi_m(x)$ . Prove that for every integer a, any prime divisor of the number 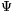$\Psi$ _m(a) either divides m or is of the form mk 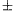$\pm$ 1.

(5 pont)

Deadline expired on November 10, 2010.

Statistics:

5 students sent a solution.

5 points: Backhausz Tibor.

4 points: Ágoston Tamás, Nagy 235 János, Nagy 648 Donát.

3 points: 1 student.

Problems in Mathematics of KöMaL, October 2010

5 students sent a solution.
5 points:	Backhausz Tibor.
4 points:	Ágoston Tamás, Nagy 235 János, Nagy 648 Donát.
3 points:	1 student.