 Problem A. 543. (October 2011)
Problem A. 543. (October 2011)
A. 543. The sum of the probabilities of some (finitely many) independent events is 4. Prove that with probability higher than 1/2, the number of occurred events is congruent to 0 or 3 modulo 4.
(Suggested by Endre Csóka, Budapest)
(5 pont)
Deadline expired on November 10, 2011.
Solution. Let the probabilities be p1,...,pn, where p1+...+pn=4. Let xj=1 if the jth event occurs, otherwise let xj=0. Let N=x1+...+xn be the number of occuring events and let (r=0,1,2,3). We have to show that q0+q3>q1+q2.
Consider the random complex number S=iN. This number is respectively 1, i, -1 or -i, if the remainder of N modulo 4 is 0, 1, 2, or 3.
Since
E(S)=q0+q1i+q2(-1)+q3(-i),
the statement is equivalent to
| (1) |
By the definition of S we have
The factors on the right-hand side are independent, so
Let (
). To prove (1) it is sufficient to prove
| (2) |
Leet if 0
 t<1 and let
t<1 and let . Then
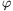 j=f(pj) for every j. We show that
j=f(pj) for every j. We show that
| (3) |
From this (2) immediately follows because
and
Let g(t)=f(t)-t. For 0<t<1 we have , the function g increases. Therefore, g(t)
 g(0)=0 and f(t)
g(0)=0 and f(t) t.
t.
Now consider the function . Since
, we have h'<0 in the intervals (0,2/7) and (5/7,1), and we have h'>0 in the interval (2/7,5/7). Therefore, h decreases in [0,2/7] and [5/7,1], and increases in [2/7,5/7]. Since h(0)=0 and
, it follows that h is never positive, so h(t)
 0 and hence
0 and hence .
Statistics:
6 students sent a solution. 5 points: Ágoston Tamás, Gyarmati Máté, Omer Cerrahoglu, Strenner Péter. 3 points: 1 student. 2 points: 1 student.
Problems in Mathematics of KöMaL, October 2011
