Problem A. 544. (October 2011)

A. 544. A circle k with center O and four distinct fixed points A, B, C, D lying on it are given. The circle k' intersects k perpendicularly at A and B. Let X be a variable point on the line OA. Let U, other than A, be the second intersection of the circles ACX and k'. Let V, other than A, be the second intersection of the circles ADX and k'. Let W, other than B, be the second intersection of the circle BDU and the line OB. Finally, let E, other than B, be the second intersection of the circles BVW and k. Prove that the location of the point E is independent from the choice of the point X.

(5 pont)

Deadline expired on November 10, 2011.

Solution. We will use the basic properties of cross ratios of quadruplets of points on lines and circles.

Let A₁ and B₁ be the points on the circle k, diametrically opposite to A and B, respectively. We show that (A₁,B,C,D)=(A,B,U,V)=(A,B₁,D,E). Then the statement follows since the points A,B₁,D and the cross ratio (A,B₁,D,E) uniquely determine the point E on the circle k.

By symmetry it is sufficient to show (A₁,B,C,D)=(A,B,U,V). Interchanging A,A₁,C,X and U by B,B₁,E,W and V, respectively, the same proof works for (A,B,U,V)=(A,B,D,E).

Place the figure in the inversive plane with the ideal point I, and apply an inversion with pole A. Denote the images of the points by A'=I,I'=A,A₁',B',C',D',X',U',V'. Since the images of circles through A are lines, the triplets of points (B',C',D'), (U',V',D'), (X',U',C') and (X',V',D') are collinear. The line AA₁X is tangent to k', therefore their images, the lines AA₁'X' and B'U'V' are parallel.

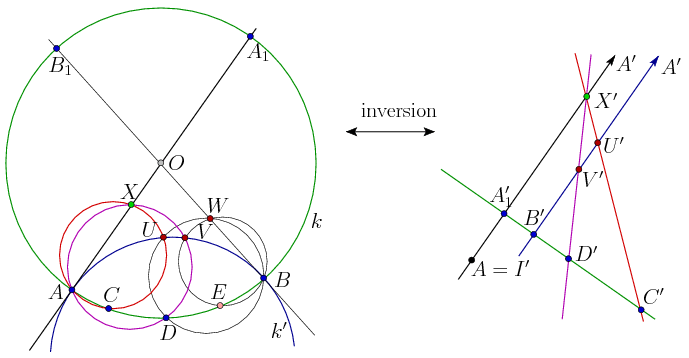
Since the inversion preserves the cross ratios and the quadruplet A₁',B',C',X' can be projected to A',B',U',V' from X', we have

(A₁,B,C,D)=(A₁',B',C',D')=(A',B',U',V')=(A,B,U,V).

Statistics:

6 students sent a solution.
5 points:	Ágoston Tamás, Gyarmati Máté, Janzer Olivér, Mester Márton, Omer Cerrahoglu, Strenner Péter.

Problems in Mathematics of KöMaL, October 2011