 Problem A. 546. (November 2011)
Problem A. 546. (November 2011)
A. 546. Show that
for every positive integer k.
(5 pont)
Deadline expired on December 12, 2011.
Solution 1. Let Un(x) be the nth Chebyshev-polynomial of the second kind, for which Un(cos t)sin t=sin ((n+1)t). The roots of U2k are the numbers ,
, ...,
and their negatives, xk+1=-x+1, xk+2=-x2, ..., x2k=-xk. On the left-hand side of the statement we have the sum of the squares of these numbers; the statement is equivalent with
| (1) |
Lemma 1. U0(x)=1, U2(x)=4x2-1, and U2k+2(x)+U2k-2(x)=(4x2-2)U2k(x) for k 1.
1.
Proof. From U0(cos t)sin t=sin t, we get U0(x)=1. Similarly, from U2(cos t)sin t=sin (3t)=(4cos2-1)sin t we get U2(x)=4x2-1.
From the identity sin (a+b)+sin (a-b)=2sin acos b we obtain
U2k+2(cos t)sin t+U2k-2(cos t)sin t=
=sin ((2k+3)t)+sin ((2k-1)t)=2sin ((2k+1)t)cos (2t)=
=2U2k(cos t)sin t.(2cos2-1),
so U2k+2(x)+U2k-2(x)=(4x2-2)U2k(x).
Lemma 2. Let . Then ak,0=(-1)k, ak,1=0 és ak,2=(-1)k+1.2k(k+1).
Proof. Apply induction on k. If k=0 then U0(x)=1, so a0,0=1=(-1)k, a0,1=0, and a0,2=0=-4k(k+1) If k=1 then U0(x)=4x2-1, so a1,0=-1=(-1)k, a1,1=0, and a1,2=4=2k(k+1). Hence, the lemma holds for k=0 and k=1.
For the induction step assume the lemma for k and (k-1). By Lemma 1,
From this we read
ak+1,0=-2.(-1)k-(-1)k-1=(-1)k+1,
ak+1,1=0,
finally
ak+1,2=4.(-1)k-2.(-1)k+1.2k(k+1)-(-1)k.2k(k-1)=
=(-1)k(4+4k(k+1)-2k(k-1))=(-1)k+2.2(k+1)(k+2).
The lemma is proved.
Now from the Viéte formulae we find
Solution 2. Let , then
 egész számra
egész számra .
From the identity we have
so
Applying again,
Therefore,
Solution 3. We use U2k again and prove (1). The polynomial can be factorized as , where c is the leading coefficient. Then
and
Substituting x=0 we obtain
| (2) |
We compute the values U2k(0), U2k'(0), U2k''(0) by differentiating
| U2k(cos t)sin t=sin ((2k+1)t) | (3a) |
twice.
| -U2k'(cos t)sin2t+U2k(cos t)cos t=(2k+1)cos ((2k+1)t), | (3b) |
| U2k''(cos t)sin3t-3U2k'(cos t)sin tcos t-U2k(cos t)sin t=-(2k+1)2sin ((2k+1)t). | (3c) |
By substituting t=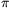 /2 in (3a--3c) we get U2k(0)=(-1)k and U2k'(0)=0, furthermore
/2 in (3a--3c) we get U2k(0)=(-1)k and U2k'(0)=0, furthermore
U2k''(0)=(-1)k-(-1)k.(2k+1)2=(-1)k+1.4k(k+1).
Plugging these into (2),
Statistics:
7 students sent a solution. 5 points: Ágoston Tamás, Gyarmati Máté, Janzer Olivér, Kovács 444 Áron, Mester Márton, Omer Cerrahoglu, Szabó 928 Attila.
Problems in Mathematics of KöMaL, November 2011
