Problem A. 552. (January 2012)

A. 552. Prove that for an arbitrary sequence $a_1,a_2,\ldots$ of nonnegative real numbers and 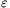$\varepsilon$ >0 there exist infinitely many positive integers n for which $n^2 \big(4a_n(1-a_{n-1})-1 \big) \le \frac14+\varepsilon$ .

(Schweitzer-competition, 2011)

(5 pont)

Deadline expired on February 10, 2012.

Solution. We prove by contradiction. Suppose that there is a sequence $a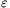_1,a_2,\ldots$ and $\varepsilon$ >0 for which

$n^2 \big(4a_n(1-a_{n-1})-1 \big) > \frac14+\varepsilon.$

(1)

holds with finitely many exception. As a simple corollary of (1) we have

4a_n(1-a_n-1)>1;

(2)

it follows that a_n>0 and a_n-1<1. Moreover, from the AM-GM inequality we get

$1 < 2\sqrt{a_n(1-a_{n-1})} \le a_n + (1-a_{n-1}),$

so a_n>a_n-1; the sequence increases from the index n₀.

By the monotonicity and boundedness the sequence converges. We show that its limit is $\frac12$ . Let $A=\lim a_n$ ; from (2) we see that

$4A(1-A) = \lim\big(4a_n(1-a_{n-1})\big) \ge 1$

(2A-1)² $\le$ 0,

therefore $A=\frac12$ . Hence, $a_n\to\frac12$ .

Define $x_n=\frac12-a_n$ . This sequence decreases from the index n₀, and it converges to 0. Transforming (1), for n>n₀ we have

$\frac{\frac14+\varepsilon}{n^2} < 4a_n(1-a_{n-1})-1 = 4\left(\frac12-x_n\right)\left(\frac12+x_{n-1}\right) - 1 = 2(x_{n-1}-x_n)-4x_{n-1}x_n$

$x_{n-1}-x_n > \frac{\frac14+\varepsilon}{2n^2} + 2x_{n-1}x_n > \frac1{8n^2}.$

(3)

Summing up (3), for n>n₀ we get a lower bound for x_n:

$x_n = \sum_{i=n+1}^\infty (x_{i-1}-x_i) > \sum_{i=n+1}^\infty \frac1{8i^2} > \sum_{i=n+1}^\infty \frac18 \left(\frac1i-\frac1{i+1}\right) = \frac1{8(n+1)}.$

(4)

In the rest of the solution we consider the properties of the sequence (n+1)x_n. We distinguish two cases.

Case 1: the sequence (n+1)x_n has a finite accumulation point. Since $(n+1)x_n>\frac18$ except for finitely many indices, all accumulation points lie in the interval $[\frac18,\infty)$ . It is well-known that there is a minimal accumulation point; this point is called as the limes inferior of the sequence. Denote by c the smallest accumulation point. Then there is a sequence $n_1<n_2<\ldots$ of indices such that $(n_k+1) x_{n_k}\to c \ge\frac18$ .

Since there is no smallest accumulation point than c, for all 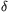$\delta$ >0, by the Bolzano-Weierstrass theorem, (n+1)x_n>c- 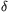$\delta$ holds except for finitely many indices. Substuting this into (3) and summing up again, we obtain that for n_k>n₀ and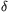 $\delta$ $\le$ c,

$(n_k+1) x_{n_k} = (n_k+1) \sum_{i=n_k+1}^\infty (x_{i-1}-x_i) > (n_k+1) \sum_{i=n_k+1}^\infty \left(\frac{\frac14+\varepsilon}{2i^2} + 2x_{i-1}x_i \right) >$

$> (n_k+1) \sum_{i=n_k+1}^\infty \left(\frac{\frac14+\varepsilon}{2i(i+1)} + 2\frac{(c-\delta)^2}{i(i+1)}\right) =$

$= \left(\frac{\frac14+\varepsilon}2+2(c-\delta)^2\right) (n_k+1) \sum_{i=n_k+1}^\infty \left(\frac1i-\frac1{i+1}\right) = \frac{\frac14+\varepsilon}2+2(c-\delta)^2.$

From the transition k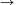 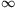$\to$ $\infty$ we get

$c = \lim (n_k+1) x_{n_k} \ge \frac{\frac14+\varepsilon}2+2(c-\delta)^2.$

Then from 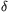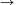$\delta$ $\to$ +0, we obtain

$c \ge \frac{\frac14+\varepsilon}2+2c^2$

$\left(2c-\frac12\right)^2 + \varepsilon \le 0,$

contradiction.

Case 2: The sequence (n+1)x_n has no accumulation point. By the Bolzano-Weierstrass theorem and the positivity this means that for all real K, (n+1)x_n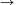 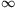$\to$ $\infty$ with finitely many exceptions, so (n+1)x_n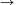 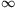$\to$ $\infty$ . Then there is an index n>n₀ such that 1<nx_n-1<(n+1)x_n. Applyinig (3),

$0< x_{n-1}-x_n - 2x_{n-1}x_n = \frac1{n+1}\Big(nx_{n-1}-(n+1)x_n\Big) + \frac{x_{n-1}}{n+1}\Big(1-2(n+1)x_n\Big),$

we get a contradiction, since both nx_n-1-(n+1)x_n and 1-2(n+1)x_n are negative.

Remark. The term 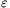$\varepsilon$ in the problem statement is important. Ommiting this quantity the statement would be false. For example, for the sequence $a_n=\frac{n}{2n+1}$ ,

$n^2 \big(4a_n(1-a_{n-1})-1 \big) = n^2 \left(\frac{4n}{2n+1}\bigg(1-\frac{n-1}{2n-1}\bigg)-1\right) = \frac{n^2}{4n^2-1} > \frac14.$

Statistics:

6 students sent a solution.

5 points: Ágoston Tamás, Mester Márton, Omer Cerrahoglu, Strenner Péter.

1 point: 2 students.

Problems in Mathematics of KöMaL, January 2012

6 students sent a solution.
5 points:	Ágoston Tamás, Mester Márton, Omer Cerrahoglu, Strenner Péter.
1 point:	2 students.

Already signed up?
New to KöMaL?