 Problem A. 553. (January 2012)
Problem A. 553. (January 2012)
A. 553. Suppose that in a simple graph G with n vertices the minimal degree 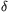 (G) is at least 3n/4. Prove that for any 2-coloring of the edges of G, there is a connected subgraph with at least
(G) is at least 3n/4. Prove that for any 2-coloring of the edges of G, there is a connected subgraph with at least 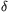 (G)+1 vertices whose edges have the same color.
(G)+1 vertices whose edges have the same color.
(Schweitzer-competition, 2011)
(5 pont)
Deadline expired on February 10, 2012.
Statistics:
6 students sent a solution. 5 points: Ágoston Tamás, Gyarmati Máté, Janzer Olivér, Mester Márton, Omer Cerrahoglu, Strenner Péter.
Problems in Mathematics of KöMaL, January 2012
