 Problem A. 554. (February 2012)
Problem A. 554. (February 2012)
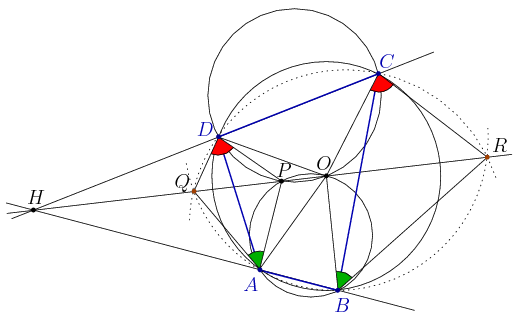
A. 554. The circumcenter of the cyclic quadrilateral ABCD is O. The second intersection point of the circles ABO and CDO, other than O, is P, which lies in the interior of the triangle DAO. Choose a point Q on the extension of OP beyond P, and a point R on the extension of OP beyond O. Prove that  QAP=
QAP= OBR holds if and only if
OBR holds if and only if  PDQ=
PDQ= RCO.
RCO.
(5 pont)
Deadline expired on March 12, 2012.
Solution. Let H be the radical center of the circles ABCD, ABOP and CDPO. Then the radical axes of any two of there cirlces, i.e. the lines AB, CD és OP pass through H. Since P lines on the shorter arcs AO and DO, it follows that H lies on the extension of OP beyond P. The radical center satisfies
| HA.HB=HC.HD=HO.HP. | (1) |
Since the quadrilateral ABOP is cyclic,
QAB +BRQ
+BRQ =(PAB
=(PAB +QAP
+QAP )+(BOP
)+(BOP -OBR
-OBR )=
)=
=(PAB +BOP
+BOP )+(QAP
)+(QAP -OBR
-OBR )=180o+(QAP
)=180o+(QAP -OBR
-OBR ).
).
Therefore, QAP =OBR
=OBR holds if and only if the quadrilateral ABRQ is cyclic, which is equivalent to HQ.HR=HA.HB.
holds if and only if the quadrilateral ABRQ is cyclic, which is equivalent to HQ.HR=HA.HB.
Similarly, QAP =OBR
=OBR holds if and only if HQ.HR=HC.HD.
holds if and only if HQ.HR=HC.HD.
Combining with (1),
Statistics:
7 students sent a solution. 5 points: Ágoston Tamás, Gyarmati Máté, Janzer Olivér, Machó Bónis, Mester Márton, Omer Cerrahoglu, Strenner Péter.
Problems in Mathematics of KöMaL, February 2012
