 Problem A. 556. (February 2012)
Problem A. 556. (February 2012)
A. 556. Prove that for arbitrary real numbers there exist a real t such that
(5 pont)
Deadline expired on March 12, 2012.
Solution. Define the function and let
. We will show that
. Then it follows that at least one of the choices t=a1, ..., t=an proves the statement.
The role of a1,...,an is symmetric and the function |sin x| is periodic by 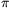 , so without loss of generality we may assume
, so without loss of generality we may assume . Define a0=0 too; then f(a0)=f(an).
If , then
, and the statement is trivial. In the rest of the solution we assume a1<
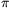 as well; then
as well; then .
By the periodicity of |sin x|,
| (1) |
Now we prove that
| (2) |
for all 1 k
k n.
n.
We prove (2) termwise. For each index 1 i
i n,
n,
In the interval [ak-1,ak] the function sin (x-ai) has constant sign: it is nonnegative for i k-1, and nonpositive for i
k-1, and nonpositive for i k. Multiplying by (-1) for i<k and summing up we obtain (2).
k. Multiplying by (-1) for i<k and summing up we obtain (2).
Combining (1) and (2), and applying Jensen's inequality to the tangent function (which is convex in [0,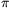 /2), we get
/2), we get
Statistics:
6 students sent a solution. 5 points: Gyarmati Máté, Janzer Olivér, Omer Cerrahoglu. 4 points: Machó Bónis. 0 point: 2 students.
Problems in Mathematics of KöMaL, February 2012
