Problem A. 564. (May 2012)

A. 564. Let k be the incircle in the triangle ABC, which is tangent to the sides AB, BC, CA at the points C₀, A₀ and B₀, respectively. The angle bisector starting at A meets k at A₁ and A₂, the angle bisector starting at B meets k at B₁ and B₂; AA₁<AA₂ and BB₁<BB₂. The circle k₁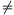k is tangent externally to the side CA at B₀ and it is tangent to the line AB. The circle k₂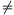k is tangent externally to the side BC at A₀, and it is tangent to the line AB. The circle k₃ is tangent to k at A₁, and it is tangent to k₁ at point P. The circle k₄ is tangent to k at B₁, and it is tangent to k₂ at point Q. Prove that the radical axis between the circles A₁A₂P and B₁B₂Q is the angle bisector starting at C.

(5 pont)

Deadline expired on June 11, 2012.

Statistics:

1 student sent a solution.
5 points:	Mester Márton.

Problems in Mathematics of KöMaL, May 2012